题目内容
【题目】直角三角形两条边长分别是6和8,则连接两条直角边中点的线段长是( )
A.3
B.5
C.4或5
D.5或3
【答案】C
【解析】解:分两种情况: ①8是直角边,如图:点E、F分别是直角边AC、BC的中点,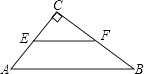
∴EF是Rt△ABC的中位线,
∴EF= ![]() AB;
AB;
在Rt△ABC中,根据勾股定理知,AB= ![]() =10,
=10,
∴EF=5;
②8是斜边,如图:点D、E分别是直角边BC、AC的中点,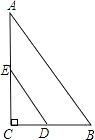
∴EF是Rt△ABC的中位线,
∴EF= ![]() AB=4.
AB=4.
综上可知连接两条直角边中点的线段长是5或4.
故选C.
【考点精析】通过灵活运用勾股定理的概念和三角形中位线定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半即可以解答此题.

练习册系列答案
相关题目