题目内容
【题目】在平面直角坐标系中,已知直线AB 与y轴交于点A,与x轴交于点B,与双曲线y= ![]() (x>0)交于点C(1,6)和点D(3,n).作CE⊥y轴于E,DF⊥x轴于F.
(x>0)交于点C(1,6)和点D(3,n).作CE⊥y轴于E,DF⊥x轴于F.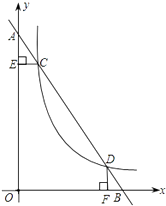
(1)求出m、n的值;
(2)求出直线AB的解析式;
(3)是否有△AEC≌△DFB,并说明理由.
【答案】
(1)
解:∵点C(1,6)和点D(3,n),
∴依题意得:m=6×1=6,
则n= ![]() =2,
=2,
故m=6,n=2

(2)
解:设直线AB的函数解析式为y=kx+b(k≠0)
由题意得 ![]() ,
,
解得: ![]() .
.
故直线AB的解析式为y=﹣2x+8
(3)
解:有△AEC≌△DFB,理由如下:
∵y=﹣2x+8
当x=0时,y=8;
当y=0时,﹣2x+8=0,
解得:x=4;
∴A(0,8),B (4,0),
∵CE⊥y轴于E,DF⊥x轴于F,
∴∠AEC=∠DFB=90°
∵A(0,8),B (4,0)C(1,6),D(3,2),
∴AE=8﹣6=2,DF=2,CE=1,BF=4﹣3=1,
∴AE=DF,CE=BF,
在△AEC和△DFB中,
 ,
,
∴△AEC≌△DFB(SAS).
【解析】(1)直接将C点坐标代入反比例函数解析式,进而得出m的值,进而求出n的值;(2)直接利用待定系数法求出直线AB的解析式;(3)利用已知解析式求出AE=DF,CE=BF,进而利用全等三角形的判定得出答案.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目