Question

【题目】如图，点A的坐标为（0，1），点B是x轴正半轴上的一动点，以AB为边作等腰直角△ABC，使∠BAC=90°，取BC的中点P．当点B从点O向x轴正半轴移动到点M（2，0）时，则点P移动的路线长为 ．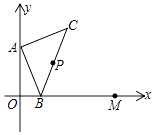

Answer 1

【答案】
【解析】解：如图所示，过P作PD⊥x轴于D，作PE⊥y轴于E，则∠DPE=90°，∠AEP=∠BDP=90°，
连接AP，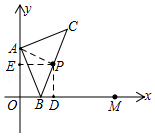

∵△ABC是等腰直角三角形，P是BC的中点，
∴AP= BC=BP，且AP⊥BC，即∠APB=90°，
∴∠APE=∠BPD，
在△AEP和△BDP中，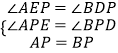
，
∴△AEP≌△BDP（AAS），
∴PE=PD，
∴点P的运动路径是∠AOM的角平分线，
如图所示，当点B与点O重合时，AB=AO=1，OC= ，
∴OP= OC= ；

如图所示，当点B与点M重合时，过P作PD⊥x轴于D，作PE⊥y轴于E，连接OP，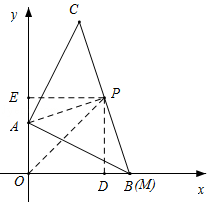

由△AEP≌△BDP，可得AE=BD，
设AE=BD=x，则OE=1+x，OD=2﹣x，
∵矩形ODPE中，PE=PD，
∴四边形ODPE是正方形，
∴OD=OE，即2﹣x=1+x，
解得x= ，
∴OD=2﹣ = ，
∴等腰Rt△OPD中，OP= OD= ，
∴当点B从点O向x轴正半轴移动到点M时，则点P移动的路线长为 ﹣ = ．
所以答案是： ．
【考点精析】掌握等腰直角三角形和角的平分线判定是解答本题的根本，需要知道等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；可以证明三角形内存在一个点，它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点)．