题目内容
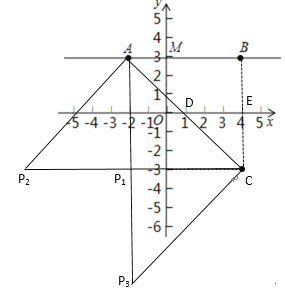
【题目】如图 ,在平面直角坐标系中,直线AB∥ x轴,线段AB与 y 轴交于点M ,已知点 A的坐标是(-2,3), BM4,点C 与点 B 关于 x 轴对称.

(1)在图中描出点C ,并直接写出点 B 和点C 的坐标:B ,C ;
(2)联结 AC 、BC ,AC 与 x 轴交于点 D ,试判断△ABC 的形状,并直接写出点 D的坐标;
(3)在坐标平面内, x 轴的下方,是否存在这样的点 P ,使得△ACP 是等腰直角三角形?如果存在,直接写出点P 的坐标;如果不存在,试说明理由.
【答案】(1)点C见解析,B(4,3),C(4,-3); (2)△ABC 是等腰直角三角形,点 D(1,0); (3)存在点 P,使得△ ACP 是等腰直角三角形,点 P1 (-2,-3)或 P2 (-8,-3)或 P3 (-2,-9).
【解析】
(1)根据点C与点B关于x轴对称描出点C即可得坐标;
(2)根据点坐标求出线段AB、BC的长度,依据∠ABC=90即可确定△ABC是等腰直角三角形,然后求出DE=CE=3可得点D的坐标;
(3)分三种情况作出图形,进而确定点P的坐标即可.
解:(1)如图,可知点B(4,3),C(4,-3);
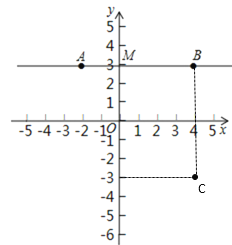
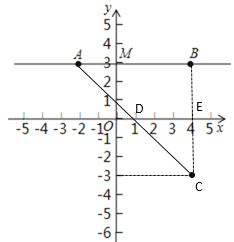
(2)如图,
∵B(4,3),
∴AB=6,
∵C(4,-3),BC⊥x轴,
∴BC=6,
∴AB=BC,∠ABC=90,
∴△ABC是等腰直角三角形,
设BC交x轴于点E,则∠DEC=90,OE=4,
∵∠DCE=45,
∴DE=CE=3,
∴OD=OE-DE=4-3=1,
∴D(1,0);
(3))存在点 P,使得△ACP 是等腰直角三角形,如图,
①当∠APC是直角时,P1(-2,-3);
②当∠PAC是直角时,P2(-8,-3);
③当∠PCA是直角时,P3(-2,-9),
故点 P1 (-2,-3)或 P2 (-8,-3)或 P3 (-2,-9).