题目内容
【题目】如图1,△ABC和△ADE都是等边三角形.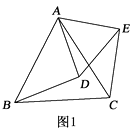
(1)求证:BD=CE;
(2)如图2,若BD的中点为P , CE的中点为Q , 请判断△APQ的形状,并说明理由.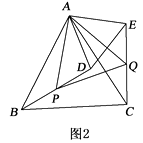
【答案】
(1)证明:∵ △ABC和△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC =∠DAE=60°.
∴∠BAC-∠DAC =∠DAE-∠DAC,即∠BAD =∠CAE.
在△ABD与△ACE中 , 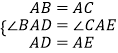
∴△ABD≌△ACE(SAS)
∴BD=CE
(2)解:△APQ是等边三角形,理由如下
∵P是BD中点,Q是CE中点,BD=CE,∴BP=CQ .
∵△ABD≌△ACE ∴∠ABP=∠ACQ .
在△ABP与△ACQ中 ∵ 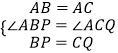 ∴△ABP≌△ACQ(SAS),
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ ,
∴∠BAP+∠CAP =∠CAQ+∠CAP,
∴∠PAQ=∠BAC=60°
∴△APQ是等边三角形
【解析】第1小题,根据两个等边三角形得到AB=AC,AD=AE,∠BAC =∠DAE=60°,然后用边角边可证明△ABD≌△ACE,问题得证;第2小题,由第1问的结论和第2问的已知条件可证△ABP≌△ACQ,得到AP=AQ,∠BAP=∠CAQ,从而可得∠PAQ=∠BAC=60°,于是问题可得证。

练习册系列答案
相关题目