��Ŀ����
����Ŀ����ͼ���ھ���ABCD�У�AB=1cm��AD=3cm����Q��A���������1cm/s���ٶ���AD���յ�D�˶�����P�ӵ�C��������1cm/s���ٶ���CB���յ�B�˶���������������һ�㵽���Լ����յ�ʱ����һ��Ҳֹͣ�˶�������ͬʱ�������˶���t��.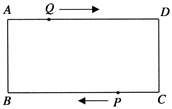
��1����0��t��3���ж��ı���BQDP����״����˵��������
��2�����ı���BQDP������S���˶�ʱ��t�ĺ�����ϵʽ��
��3������tΪ��ֵʱ���ı���BQDPΪ����.
���𰸡�
��1���⣺���ı���ABCD�Ǿ��Σ���AD//BC.
�ߵ�Q�ӵ�A��������1cm/s���ٶ���AD���յ�D�˶���
ͬʱ����P�ӵ�C��������1cm/s���ٶ���CB���յ�B�˶���
��QD=BP��
���ı���BPDQ��ƽ���ı���
��2���⣺��BP=9-t�����ı���BQDP�����S=BPAB=��3-t����1=3-t=-t+3
��3���⣺��һ���ڱ���ȵ�ƽ���ı��������Σ���BQ=PQ.
��AQ=t��AB=1�� ![]() ,QD=3-t
,QD=3-t
![]()
��֮�� ![]()
����������1�����ı���ABCD�Ǿ��Σ��õ��Ա�AD//BC����Q�ӵ�A��������1cm/s���ٶ���AD���յ�D�˶���ͬʱ����P�ӵ�C��������1cm/s���ٶ���CB���յ�B�˶����õ�QD=BP������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ��õ�BPDQ��ƽ���ı��Σ���2����BP=9-t���õ��ı���BQDP�����S=BPAB���õ��ı���BQDP������S���˶�ʱ��t�ĺ�����ϵʽ����3����һ���ڱ���ȵ�ƽ���ı��������Σ���֪BQ=PQ���������εĶԽ����ഹֱƽ�֣��ٸ��ݹ��ɶ��������BQ�Ĵ���ʽ����QD=3-t�����t��ֵ.