题目内容
【题目】如图,直线l1的函数解析式为y=﹣2x+4,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.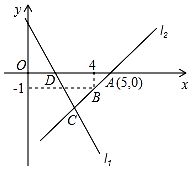
(1)求直线l2的函数解析式;
(2)求△ADC的面积;
(3)在直线l2上是否存在点P,使得△ADP面积是△ADC面积的2倍?如果存在,请求出P坐标;如果不存在,请说明理由.
【答案】
(1)解:设直线l2的函数解析式为y=kx+b,
将A(5,0)、B(4,﹣1)代入y=kx+b,
![]() ,解得:
,解得: ![]() ,
,
∴直线l2的函数解析式为y=x﹣5
(2)解:联立两直线解析式成方程组,
![]() ,解得:
,解得: ![]() ,
,
∴点C的坐标为(3,﹣2).
当y=﹣2x+4=0时,x=2,
∴点D的坐标为(2,0).
∴S△ADC= ![]() AD|yC|=
AD|yC|= ![]() ×(5﹣2)×2=3
×(5﹣2)×2=3
(3)解:假设存在.
∵△ADP面积是△ADC面积的2倍,
∴|yP|=2|yC|=4,
当y=x﹣5=﹣4时,x=1,
此时点P的坐标为(1,﹣4);
当y=x﹣5=4时,x=9,
此时点P的坐标为(9,4).,只需
综上所述:在直线l2上存在点P(1,﹣4)或(9,4),使得△ADP面积是△ADC面积的2倍.
【解析】第1小题,所求直线经过A、B两点,把y=kx+b这两点的坐标代入可求解;第2小题,要求三角形ADC的面积,只需求出C、D两点的坐标,点C是已知两直线的交点,联立解方程组可得坐标,点D是直线y=﹣2x+4与x轴的交点,问题的解;第3小题,这是一个存在性问题,假定存在,根据△ADP面积是△ADC面积的2倍计算,有解即存在,否则不存在。

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且 ![]() =8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
=8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
(1)乙运动员射击训练成绩的众数是 , 中位数是 .
(2)求甲运动员射击成绩的平均数,并判断甲、乙两人在本次射击成绩的稳定性.