题目内容
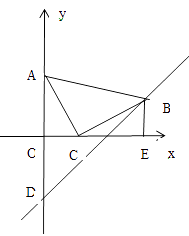
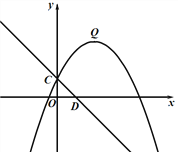
【题目】如图,抛物线![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得⊿CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由.
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。

【答案】(1)![]() (2)符合题意的M有三点,分别是(2 , 3 ),(
(2)符合题意的M有三点,分别是(2 , 3 ),(![]() ,
, ![]() ),(
),( ![]() ,
, ![]() ) (3)存在,在P点和F点移动过程中,△PCF的周长存在最小值,最小值为2
) (3)存在,在P点和F点移动过程中,△PCF的周长存在最小值,最小值为2![]() .
.
【解析】(1)设抛物线的解析式为y=a(x-2)2+3. 将C(0,1)代入求得a的值即可;
(2)①C为直角顶点时,作CM⊥CD,CM交抛物线与点M,先求得直线CD的解析式,然后再求得直线CM的解析式,然后求得CM与抛物线的交点坐标即可;②D为直角顶点坐标时,作DM⊥CD,先求得直线CM的解析式,然后将直线CM与抛物线的交点坐标求出即可;
(3)存在. 作点C关于直线QE的对称点C/,作点C关于x轴的对称点C//,连接C/C//,交QE于点P,则△PCE即为符合题意的周长最小的三角形,由对称轴的性质可知,△PCE的周长等于线段C/C//的长度,然后过点C/作C/N⊥y轴,然后依据勾股定理求得C/C//的长即可.
解:(1)设抛物线的解析式为![]()
将C(0,1)代入得: ![]()
解得: ![]()
∴![]()
(2)①C为直角顶点时
如图①:CM⊥CD

设直线CD为![]() ,
,
∵OD=OC
∴OD=1
∴D(1,0)
把D(1,0)代入![]() 得:
得: ![]()
∴![]()
∵CM⊥CD,
∴易得直线CM为: ![]()
则: 
解之得:M(2 , 3 ),恰好与Q点重合.分
②D为直角顶点时:
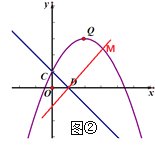
如图②,易得:直线DM为![]()
则: 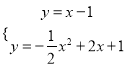
则M为(![]() ,
, ![]() )或 (
)或 ( ![]() ,
, ![]() )
)
综上所述,符合题意的M有三点,分别是(2 , 3 ),(![]() ,
, ![]() ),(
),( ![]() ,
, ![]() ).
).
(3) 在.
如图③所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.

(证明如下:不妨在线段OD上取异于点F的任一点F′,在线段QE上取异于点P的任一点P′,连接F′C″,F′P′,P′C′.
由轴对称的性质可知,△P′CF′的周长=F′C″+F′P′+P′C′;
而F′C″+F′P′+P′C′是点C′,C″之间的折线段,
由两点之间线段最短可知:F′C″+F′P′+P′C′>C′C″,
即△P′CF′的周长大于△PCE的周长.)
如答图④所示,连接C′E,

∵C,C′关于直线QE对称,△QCE为等腰直角三角形,
∴△QC′E为等腰直角三角形,
∴△CEC′为等腰直角三角形,
∴点C′的坐标为(4,5);
∵C,C″关于x轴对称,∴点C″的坐标为(0,﹣1).
过点C′作C′N⊥y轴于点N,则NC′=4,NC″=4+1+1=6,
在Rt△C′NC″中,由勾股定理得:C′C″=![]() =2
=2![]() .
.
综上所述,在P点和F点移动过程中,△PCF的周长存在最小值,最小值为2![]() .
.
“点睛”本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求函数的解析式,掌握相互垂直的两条直线的一次项系数乘积为-1是解答问题(2)的关键,利用轴对称的性质将三角形的周长转化为线段C/C//的长是解答问题(3)的关键.

 阅读快车系列答案
阅读快车系列答案