题目内容
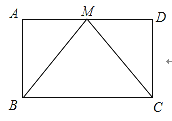
【题目】如图,在ABCD中,M为AD的中点,BM=CM.
求证:(1)△ABM≌△DCM;
(2)四边形ABCD是矩形.
【答案】(1)详见解析;(2)详见解析;
【解析】
(1)由四边形ABCD是平行四边形,得出AB=CD,又由M为AD的中点,得出AM=MD,又AB=CD,AM=MD,BM=CM,故△ABM ≌△DCM(SSS);
(2)根据(1)中△ABM≌△DCM,得出∠BAD=∠CDA,又四边形ABCD是平行四边形,∠BAD+∠CDA=180°,得出∠BAD=∠CDA=90°,故可判定四边形ABCD是矩形.
证明:(1)∵四边形ABCD是平行四边形
∴AB=CD
∵M为AD的中点
∴AM=MD
∵AB=CD,AM=MD,BM=CM
∴△ABM ≌△DCM(SSS)
(2)∵△ABM≌△DCM
∴∠BAD=∠CDA
又∵四边形ABCD是平行四边形
∵∠BAD+∠CDA=180°
∴∠BAD=∠CDA=90°
∴四边形ABCD是矩形.

练习册系列答案
相关题目