题目内容
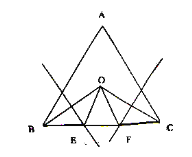
【题目】如图所示,在等边三角形ABC中,∠B、∠C 的平分线交于点O,OB和OC的垂直平分线交BC于E、F,求证:BE=EF=FC
【答案】见解析
【解析】
先根据线段的垂直平分线的性质和角平分线性质得到有关的角和线段之间的等量关系:∠OBC=∠OCB=30°,OE=BE,OF=FC;再利用三角形的外角等于不相邻的两内角和求出∠OEF=60°,∠OFE=60°.从而判定△OEF是等边三角形即OE=OF=EF,通过线段的等量代换求证即可.
解:在等边三角形ABC中.
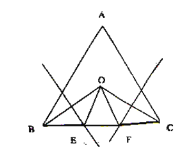
∵∠ABC、∠ACB的平分线交于点O,OB和OC的垂直平分线交BC于E、F,
∴∠OBC=∠OCB=30°,OE=BE,OF=FC.
∴∠OEF=60°,∠OFE=60°.
∴OE=OF=EF.
∴BE=EF=FC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送鲜花,感恩母亲,祝福母亲. 节日前夕,某花店采购了一批鲜花礼盒,成本价为30元每件,分析上一年母亲节的鲜花礼盒销售情况,得到了如下数据,同时发现每天的销售量![]() (件)是销售单价
(件)是销售单价![]() (元/件)的一次函数.
(元/件)的一次函数.
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 350 | 300 | 250 | 200 | … |
(1)求出![]() 与
与![]() 的函数关系;
的函数关系;
(2)物价局要求,销售该鲜花礼盒获得的利润不得高于100﹪:
①当销售单价![]() 取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价);
取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价);
②试确定销售单价![]() 取何值时,花店销该鲜花礼盒每天获得的利润
取何值时,花店销该鲜花礼盒每天获得的利润![]() (元)最大?并求出花店销该鲜花礼盒每天获得的最大利润.
(元)最大?并求出花店销该鲜花礼盒每天获得的最大利润.