题目内容
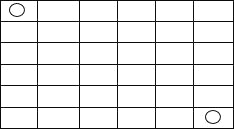
【题目】如图所示,图(1)中含“○”的矩形有1个,图(2)中含“○”的矩形有7个,图(3)中含“○”的矩形有17个,按此规律,图(6)中含“○”的矩形有( )
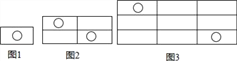
A. 70 B. 71 C. 72 D. 73
【答案】B
【解析】分析:①先计算每个图形中单个矩形的个数:图(1):12=1,图2:22=4,则图(6):62=36;
②由1个矩形中含“○”有2个,由2个矩形中含“○”有:2+2=4个(发现与2的因数有关系),由3个矩形中含“○”有:2+2=4个,…,由36个矩形中含“○”有1个,最后相加为71个.
详解:图(6)中,62=36,
1个矩形:1×2=2个,
2个矩形:1×2:2个,
2×1:2个,
3个矩形:1×3:2个
3×1:2个
4个矩形:1×4:2个
4×1:2个
2×2:2个
5个矩形:1×5:2个
5×1:2个
6个矩形:1×6:2个
6×1:2个
2×3:2个
3×2:2个
8个矩形:2×4:2个
4×2:2个
9个矩形:3×3:2个
10个矩形:2×5:2个
5×2:2个
12个矩形:2×6:2个
6×2:2个
3×4:2个
4×3:2个
15个矩形:3×5:2个
5×3:2个
16个矩形:4×4:2个
18个矩形;3×6:2个
6×3:2个
20个矩形:4×5:2个
5×4:2个
24个矩形:4×6:2个
6×4:2个
25个矩形:5×5:2个
30个矩形:5×6:2个
6×5:2个
36个矩形:6×6:1个,
总计和为71个;
故选B.

 阅读快车系列答案
阅读快车系列答案【题目】某原料仓库一天的原料进出记录如下表(运进用正数表示,运出用负数表示);
每次进出数量(单位:吨) | -3 | 4 | -1 | 2 | -5 |
进出次数 | 2 | 1 | 3 | 3 | 2 |
(1)这天仓库的原料比原来增加或减少了多少吨?
(2)根据实际情况,现有两种方案:
方案一:运进每吨原料费用5元,运出每吨原料费用8元;
方案二:不管运进还是运出费用都是每吨原料6元;
从节约运费的角度考虑,选用哪一种方案较合适?请说明理由.