题目内容
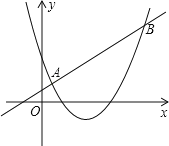
【题目】如图,正比例函数y=![]() x与一次函数y=ax+7的图象相交于点P(4,n),过点A(2,0)作x轴的垂线,交一次函数的图象于点B,连接OB.
x与一次函数y=ax+7的图象相交于点P(4,n),过点A(2,0)作x轴的垂线,交一次函数的图象于点B,连接OB.
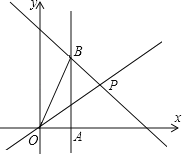
(1)求a值;
(2)求△OBP的面积;
(3)在坐标轴的正半轴上存在点Q,使△POQ是以OP为腰的等腰三角形,请直接写出Q点的坐标.
【答案】(1)a=-1;(2)7;(3)点Q的坐标为(5,0)或(8,0)或(0,5)或(0,6)
【解析】
(1)先由点P在正比例函数图象上求得n的值,再把点P坐标代入一次函数的解析式即可求出结果;
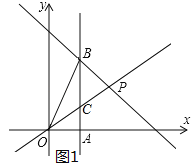
(2)易求点B坐标,设直线AB与OP交于点C,如图,则点C坐标可得,然后利用△OBP的面积=S△BCO+S△BCP代入相关数据计算即可求出结果;
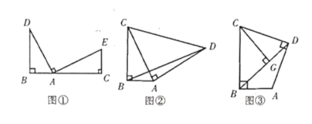
(3)先根据勾股定理求出OP的长,再分两种情况:当OP=OQ时,以O为圆心,OP为半径作圆分别交y轴和x轴的正半轴于点Q1、Q2,如图2,则点Q1、Q2即为所求,然后利用等腰三角形的定义即可求出结果;当PO=PQ时,以P为圆心,OP为半径作圆分别交y轴和x轴的正半轴于点Q4、Q3,如图3,则点Q4、Q3也为所求,然后利用等腰三角形的性质即可求得结果.
解:(1)把点P(4,n)代入y=![]() x,得:n=
x,得:n=![]() ×4=3,∴P(4,3),
×4=3,∴P(4,3),
把P(4,3)代入y=ax+7得,3=4a+7,∴a=﹣1;
(2)∵A(2,0),AB⊥x轴,∴B点的横坐标为2,
∵点B在y=﹣x+7上,∴B(2,5),
设直线AB与OP交于点C,如图1,当x=2时,![]() ,∴C(2,
,∴C(2,![]() ),
),
∴△OBP的面积=S△BCO+S△BCP=![]() 2×(5﹣
2×(5﹣![]() )+
)+![]() (4﹣2)×(5﹣
(4﹣2)×(5﹣![]() )=7;
)=7;
(3)过点P作PD⊥x轴于点D,∵P(4,3),∴OD=4,PD=3,∴![]() ,
,
当OP=OQ时,以O为圆心,OP为半径作圆分别交y轴和x轴的正半轴于点Q1、Q2,如图2,则点Q1、Q2即为所求,且Q2(5,0)、Q1(0,5);
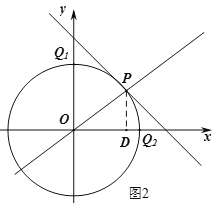
当PO=PQ时,以P为圆心,OP为半径作圆分别交y轴和x轴的正半轴于点Q4、Q3,如图3,则点Q4、Q3也为所求,
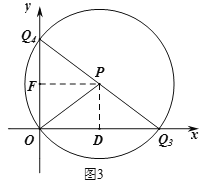
由于PO=PQ3,∴DQ3=DO=4,∴Q3(8,0),
过点P作PF⊥y轴于点F,同理可得:FQ4=FO=3,∴Q4(0,6).
综上所述,在坐标轴的正半轴上存在点Q,使△POQ是以OP为腰的等腰三角形,点Q的坐标为(5,0)或(8,0)或(0,5)或(0,6).

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案