题目内容
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() r,则称点P为⊙O的“随心点”.
r,则称点P为⊙O的“随心点”.
(1)当⊙O的半径r=2时,A(4,0),B(0,3),C(![]() ,﹣
,﹣![]() ),D(﹣
),D(﹣![]() ,﹣2)中,⊙O的“随心点”是 ;
,﹣2)中,⊙O的“随心点”是 ;
(2)若点E(6,8)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=4时,直线y=﹣x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
【答案】(1)B,D;(2)![]() ≤r≤20;(3)2≤b≤6
≤r≤20;(3)2≤b≤6![]() 或﹣6
或﹣6![]() ≤b≤﹣2
≤b≤﹣2
【解析】
(1)分别判断A、B、C、D四个点到圆心O的距离是否符合规定即可;
(2)先算出OE长度,再根据“随心点“的定义列出不等式组解出r的取值范围;
(3)r已知,因此先算出![]() r和
r和![]() r的值,由解析式y=﹣x+b可得M、N坐标,由于直线y=x与y=﹣x+b垂直,故联立两直线方程可解出交点P的坐标,然后用两点间的距离公式可得OP长度(注意b的符号未知,表示长度应加绝对值符号),线段MN上存在“随心点“,则意味着OM≥2且OP≤6,列出不等式组即可解出b的取值范围.
r的值,由解析式y=﹣x+b可得M、N坐标,由于直线y=x与y=﹣x+b垂直,故联立两直线方程可解出交点P的坐标,然后用两点间的距离公式可得OP长度(注意b的符号未知,表示长度应加绝对值符号),线段MN上存在“随心点“,则意味着OM≥2且OP≤6,列出不等式组即可解出b的取值范围.
解:(1)∵r=2,
∴![]() r=1,
r=1,![]() r=3,
r=3,
∵A(4,0),
∴OA=4>3,
∴A不是“随心点”;
∵B(0,3),
∴OB=3,
∴B是“随心点”;
∵C(![]() ,﹣
,﹣![]() ),
),
∴OC=![]() =
=![]() <1,
<1,
∴C不是“随心点”;
∵D(﹣![]() ,﹣2),
,﹣2),
∴OD=![]() =
=![]() ,
,
∴D是“随心点”;
综上所述,⊙O的“随心点”是B、D,
故答案为:B、D;
(2)∵E(6,8),
∴OE=![]() =10,
=10,
因为E是⊙O的“随心点”,
∴![]() r≤OE≤
r≤OE≤![]() r,即
r,即![]() r≤10≤
r≤10≤![]() r,
r,
解得![]() ≤r≤20;
≤r≤20;
(3)∵r=4,
∴![]() r=2,
r=2,![]() r=6,
r=6,
直线y=﹣x+b(b≠0)与x轴交于点M,与y轴交于点N,
∴M(b,0),N(0,b),
过点O且与直线y=﹣x+b垂直的直线解析式为y=x,
联立方程组:![]() ,解得:
,解得:![]() ,
,
∴直线y=﹣x+b与直线y=x交点坐标为P(![]() ,
,![]() ),
),
∴OP=![]() ,
,
∵线段MN上存在⊙O的随心点,
∴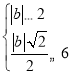 ,
,
解得2≤b≤6![]() 或﹣6
或﹣6![]() ≤b≤﹣2.
≤b≤﹣2.

【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?