Question

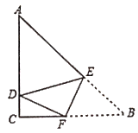
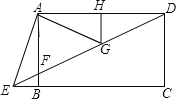
【题目】如图，四边形ABCD是矩形，点E在线段CB的延长线上，连接DE交AB于点F，∠AED＝2∠CED，点G是DF的中点．

（1）求证：AE＝AG；

（2）若BE＝2，BF＝1，AG＝5，点H是AD的中点，求GH的长．

Answer 1

【答案】（1）见解析；（2）GH＝

【解析】

（1）先由矩形的性质得对边平行及∠BAD＝90°，再由平行线的性质及直角三角形的斜边中线性质得∠CED＝∠ADB和∠ADB＝∠GAD，利用三角形的外角性质及∠AED＝2∠CED，可得∠AGE＝∠AED，从而证得结论；

（2）由（1）中结论AE＝AG及AG＝5可得AE的长；再在Rt△ABE中，由勾股定理求得AB的长；然后由AF＝AB﹣BF，求得AF的长；最后由三角形的中位线定理可求得GH的长．

解：（1）证明：∵四边形ABCD是矩形，

∴AD∥BC，∠BAD＝90°，

∴∠CED＝∠ADB，

又∵点G是DF的中点，

∴GA＝GD，

∴∠ADG＝∠GAD，

∴∠AGE＝2∠CED，

又∵∠AED＝2∠CED，

∴∠AGE＝∠AED，

∴AE＝AG；

（2）∵AE＝AG，AG＝5，

∴AE＝5，

又∵在Rt△ABE中，BE＝2，

∴AB＝＝，

∵BF＝1，

∴AF＝AB﹣BF＝﹣1，

∵G是DF中点，H是AD中点，

∴GH＝AF＝．