题目内容
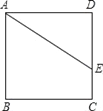
【题目】如图,在正方形ABCD中,点E在边DC上,DE=7,EC=3,把线段AE绕点A旋转后使点E落在直线BC上的点P处,则CP的长为_____.
【答案】3或17.
【解析】
分类讨论:当点P 落在边BC上时,如图,利用正方形的性质得AB=AD=DE+CE=10,∠ABF=∠D=90°,利用旋转的性质得AP=AE,则可证明Rt△ABP≌Rt△ADE,所以BP =DE=7,于是得到CP=BC-BP=3;当点P落在BC的延长线上的点P′时,如图,同样可证明Rt△ABP′≌Rt△ADE,得到BP′=DE=7,则CP′=BC+BP′=17,于是可判断P、C两点的距离为3或17.
当点P落在边BC上时,如图,
∵四边形ABCD为正方形,
∴AB=AD=DE+CE=3+2=5,∠ABP=∠D=90°,
∵线段AE绕点A旋转后使点E落在直线BC上的点F处,
∴AF=AE,
在Rt△ABP和Rt△ADE中:AP=AE,AB=AD,
∴Rt△ABP≌Rt△ADE,
∴BP=DE=7,
∴CP=BC-BP=10-7=3;
当点F落在BC的延长线上的点P′时,如图,
同样可证明Rt△ABP′≌Rt△ADE,
∴BP′=DE=7,
∴CP′=BC+BP′=10+7=17,
∴P、C两点的距离为3或17.

故答案为:3或17

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目