Question

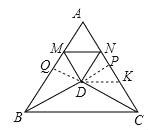
【题目】如图，△ABC是边长为5的等边三角形，△BDC是顶角为120°的等腰三角形，以D为顶点作一个60°的∠MDN，点M、N分别在AB、AC上，连接MN，则△AMN的周长为 ．

Answer 1

【答案】5．

【解析】

试题分析：延长CD、BD，分别交AB于Q，交AC于P，在AC上取一点K，使KP=QM，连接DK，

∵△BDC是顶角为120°的等腰三角形，

∴BD=CD，∠DBC=∠DCB=30°，

∵△ABC是等边三角形，

∴∠ABC=∠ACB=60°，

∴∠BPC=∠CQB=90°，

∴PC=BC，BQ=BC，

∴PC=BQ=AQ=AP=×5=，

在Rt△BDQ和Rt△CDP中，

∵ ，

∴Rt△BDQ≌Rt△CDP（HL），

∴DQ=PD，

同理得Rt△DQM≌Rt△DPK，

∴DM=DK，∠QDM=∠PDK，

∵∠BDQ=60°，∠MDN=60°，

∴∠QDM+∠NDP=60°，

∴∠PDK+∠NDP=60°，

即∠NDK=60°，

∴∠NDK=∠MDN=60°，

∵ND=ND，

∴△MDN≌△KDN，

∴MN=NK=NP+PK，

∴△AMN的周长=AM+AN+MN=AM+AN+NP+PK=AM+AN+NP+QM=AP+AQ=+=5，