��Ŀ����
����Ŀ�����壺��ƽ��ֱ������ϵ�У���Q����Ϊ��x��y����������Q��ֱ��l��x��н�Ϊ45��ʱ�����ֱ��lΪ��Q�ġ�����ֱ�ߡ���
��1����֪��A������Ϊ��6��0�������A�ġ�����ֱ�ߡ�����ʽ��
��2����֪��D������Ϊ��0����4��������D�ġ�����ֱ�ߡ�ͼ���ڶ������������ޣ�����x�ύ��C�㣬����P�ڷ���������y=![]() ��x��0���ϣ����PCD�������Сֵ����ʱ��P�����ꣻ
��x��0���ϣ����PCD�������Сֵ����ʱ��P�����ꣻ
��3����֪��M������Ϊ��0��2����������M���ڵ�һ�����������ġ�����ֱ�ߡ���������y=x2+��m��2��x+m+2�ཻ��A��x1��y1����B��x2��y2�����㣬��0��x1��2��0��x2��2����m��ȡֵ��Χ��
���𰸡���1��y=x��6��y=��x+6����2����PCD�������Сֵ��24����ʱ��P�������ǣ�4��4������3��m��ȡֵ��Χ��1��m��3��
��������
��1���ɡ�����ֱ�ߡ��Ķ���֪��ֱ��l��ֱ��y=x��y=��xƽ�У����A�ġ�����ֱ�ߡ�����ʽΪ��y=x+b��y=��x+b����A��6�� 0�����룬��0=6+b����0=��6+b���ɴ����bֵ���������A�ġ�����ֱ�ߡ�����ʽ����2������ù���D�ġ�����ֱ�ߡ�Ϊy=��x��4�������C�������Ϊ����4��0�������ɵá�OCD�ǵ���ֱ�������Σ�����CD=4![]() ����Ϊ�߶�CD�ij���Ϊ��ֵ����֪������P��ֱ����ֱ��CD��ֱʱ����PCD�������С���ɴ˼��ɽ�𣻣�3����ù���M�ġ�����ֱ�ߡ�Ϊy=x+2���������ߵĽ���ʽ����M�ġ�����ֱ�ߡ������������ɵ�x2+��m��3��x+m=0�����ݸ���ϵ���Ĺ�ϵ��x1+x2=3��m��x1x2=m����0��x1��2��0��x2��2����֪0��x1+x2��4��0��x1x2��4�ң�m��3��2��4m��0���ɴ˼������m��ȡֵ��Χ.
����Ϊ�߶�CD�ij���Ϊ��ֵ����֪������P��ֱ����ֱ��CD��ֱʱ����PCD�������С���ɴ˼��ɽ�𣻣�3����ù���M�ġ�����ֱ�ߡ�Ϊy=x+2���������ߵĽ���ʽ����M�ġ�����ֱ�ߡ������������ɵ�x2+��m��3��x+m=0�����ݸ���ϵ���Ĺ�ϵ��x1+x2=3��m��x1x2=m����0��x1��2��0��x2��2����֪0��x1+x2��4��0��x1x2��4�ң�m��3��2��4m��0���ɴ˼������m��ȡֵ��Χ.
�ɡ�����ֱ�ߡ��Ķ���֪��ֱ��l��ֱ��y=x��y=��xƽ�У�
��1�����A�ġ�����ֱ�ߡ�����ʽΪ��y=x+b��y=��x+b��
��A��6�� 0�����룬��0=6+b����0=��6+b
���b=��6��b=6��
�ʵ�A�ġ�����ֱ�ߡ�����ʽΪ��y=x��6��y=��x+6��
��2���ߵ�D������Ϊ��0����4��������D�ġ�����ֱ�ߡ�ͼ���ڶ������������ޣ�
�����D�ġ�����ֱ�ߡ�Ϊy=��x��4��
��C����4��0��������OCD�ǵ���ֱ�������Σ�
��CD=4![]() ��
��
���߶�CD�ij���Ϊ��ֵ��
�൱����P��ֱ����ֱ��CD��ֱʱ����PCD�������С��
�֡ߵ�P�ڷ���������y=![]() ��x��0��ͼ���ϣ�
��x��0��ͼ���ϣ�
���P���߶�CD�Ĵ�ֱƽ������˫���ߵĽ��㣬��ͼ��
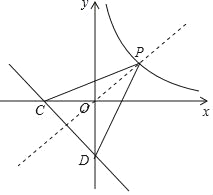
��ֱ��CD��ֱ��y=��xƽ�У�
���P��ֱ��y=x�ϣ�
����P��a��a����
��a=![]() ��
��
���a=4����ȥ��ֵ����
��ʱP��4��4����
S��PCD=![]() ��4
��4![]() ����4
����4![]() +2
+2![]() ��=24��
��=24��
������������PCD�������Сֵ��24����ʱ��P�������ǣ�4��4����
��3���ߵ�M������Ϊ��0��2��������M�ġ�����ֱ�ߡ�������һ�����������ޣ�
�����M�ġ�����ֱ�ߡ�Ϊy=x+2��
��������֪��![]()
��������x2+��m��3��x+m=0
��x1+x2=3��m��x1x2=m��
��0��x1��2��0��x2��2��
��0��x1+x2��4��0��x1x2��4�ң�m��3��2��4m��0��
��0��3��m��4��0��m��4�ң�m��3��2��4m��0��
��ã�1��m��3��
��m��ȡֵ��Χ��1��m��3��

 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�