题目内容
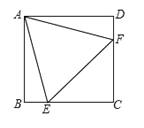
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点![]() 分别在BC和CD上,下列结论:
分别在BC和CD上,下列结论:
(1)BE=DF;(2)∠AEB=75°;(3)BE+DF=EF;(4)![]() .
.
其中正确的序号是____________(把你认为正确的序号都填上)
【答案】①②④
【解析】
根据三角形的全等的知识可以判断①的正误;根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;根据线段垂直平分线的知识可以判断③的正误,利用解三角形求正方形的面积等知识可以判断④的正误.
解:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接ACAC,交EFEF于GG点,

∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF=√2∴CE=CF=2,
设正方形的边长为a,
在Rt△ADF中,
AD2+DF2=AF2,即a2+(a√2)2=4,
解得a= ![]() ,
,
则a2=2+![]() ,
,
S正方形ABCD=2+![]() ,④说法正确.
,④说法正确.
故答案为①②④.

【题目】某学校对学生暑假参加志愿服务的时间进行抽样调查,将收集的数据分成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五组进行整理,并绘制成如下的统计图表(图中信息不完整).
五组进行整理,并绘制成如下的统计图表(图中信息不完整).
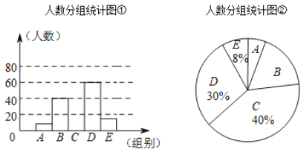
分组统计表
组别 | 志愿服务时间 | 人数 |
A |
|
|
B |
| 40 |
C |
|
|
D |
|
|
E |
| 16 |
请结合以上信息解答下列问题
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)补全“人数分组统计图①中![]() 组的人数和图②
组的人数和图②![]() 组和
组和![]() 组的比例值”;
组的比例值”;
(3)若全校学生人数为800人,请估计全校参加志愿服务时间在![]() 的范围的学生人数.
的范围的学生人数.