题目内容
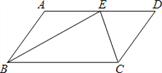
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10, ![]() =
= ![]() =
= ![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )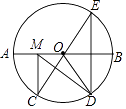
A.1
B.2
C.3
D.4
【答案】C
【解析】∵ ![]() =
= ![]() =
= ![]() ,点E是点D关于AB的对称点,
,点E是点D关于AB的对称点,
∴ ![]() =
= ![]() ,
,
∴∠DOB=∠BOE=∠COD= ![]() =60°,∴①正确;
=60°,∴①正确;
∠CED= ![]() ∠COD=
∠COD= ![]() =30°=
=30°= ![]() ,∴②正确;
,∴②正确;
∵ ![]() 的度数是60°,
的度数是60°,
∴ ![]() 的度数是120°,
的度数是120°,
∴只有当M和A重合时,∠MDE=60°,
∵∠CED=30°,
∴只有M和A重合时,DM⊥CE,∴③错误;
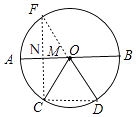
做C关于AB的对称点F,连接CF,交AB于N,连接DF交AB于M,此时CM+DM的值最短,等于DF长,
连接CD,
∵ ![]() =
= ![]() =
= ![]() =
= ![]() ,并且弧的度数都是60°,
,并且弧的度数都是60°,
∴∠D= ![]() =60°,∠CFD=
=60°,∠CFD= ![]() =30°,
=30°,
∴∠FCD=180°﹣60°﹣30°=90°,
∴DF是⊙O的直径,
即DF=AB=10,
∴CM+DM的最小值是10,∴④正确;
故答案为:C.
由已知条件求出,求出∠DOB=∠COD=∠BOE=60°,求出∠CED,即可判断①②;根据圆周角定理求出当M和A重合时∠MDE=60°即可判断③;求出M点的位置,根据圆周角定理得出此时DF是直径,即可求出DF长,即可判断④,最后得到所求的结论..

练习册系列答案
相关题目