题目内容
【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离![]() .例如P1(2,-4)、P2(7,8),其两点间的距离
.例如P1(2,-4)、P2(7,8),其两点间的距离![]() ,同时,当两点所在的直线再坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线再坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离____.
(2)已知M、N在平行于y轴的直线上,点M的纵坐标为4,点N的纵坐标为-1,试求M、N 两点的距离为 .
(3)已知一个三角形各顶点坐标为D(1,6)、E(-2,2)、F(4,2),你能判定此三角形的形状吗?说明理由.
(4)在(3)的条件下,平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标及PD+PF的最短长度.
【答案】(1)13;(2)5;(3)△DEF为等腰三角形;(2)图详见解析,P(![]() ,0),PD+PF最短为
,0),PD+PF最短为![]() .
.
【解析】
(1)根据阅读材料中的A与B的坐标,利用两点间的距离公式求出A与B的距离即可;
(2)根据两点在平行于y轴的直线上,由M与N的纵坐标求出MN的距离即可;
(3)由三顶点坐标求出DE,DF,EF的长,即可判定此三角形形状;
(4)找出F关于x轴的对称点F′,连接DF′,与x轴交于P点,此时PD+PF最短,设直线DF′的解析式为y=kx+b,将D与F′的坐标代入求出k与b的值,确定出直线DF′解析式,令y=0求出x的值,确定出P坐标,由D与F′坐标,利用两点间的距离公式求出DF′的长,即为PD+PF的最短长度.
(1)∵A(2,4)、B(﹣3,﹣8),∴AB![]() 13;
13;
(2)∵M、N在平行于y轴的直线上,点M的纵坐标为4,点N的纵坐标为﹣1,∴MN=|4﹣(﹣1)|=5;
(3)△DEF为等腰三角形,理由为:
∵D(1,6)、E(﹣2,2)、F(4,2),∴DE![]() 5,DF
5,DF![]() 5,EF
5,EF![]() 6,即DE=DF,则△DEF为等腰三角形;
6,即DE=DF,则△DEF为等腰三角形;
(4)作F关于x轴的对称点F′,连接DF′,与x轴交于点P,此时DP+PF最短,设直线DF′解析式为y=kx+b,将D(1,6),F′(4,﹣2)代入得:![]() ,解得:
,解得: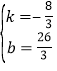 ,∴直线DF′解析式为y
,∴直线DF′解析式为y![]() ,令y=0,得:x
,令y=0,得:x![]() ,即P(
,即P(![]() ,0).
,0).
∵PF=PF′,∴PD+PF=DP+PF′=DF′![]() ,则PD+PF的长度最短时点P的坐标为(
,则PD+PF的长度最短时点P的坐标为(![]() ,0),此时PD+PF的最短长度为
,0),此时PD+PF的最短长度为![]() .
.