题目内容
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.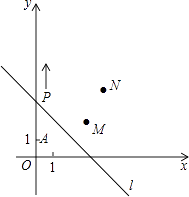
(1)当t=2时,则AP= , 此时点P的坐标是 .
(2)当t=3时,求过点P的直线l:y=﹣x+b的解析式?
(3)当直线l:y=﹣x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 .
【答案】
(1)2,(0,3)
(2)解:∵当t=3时,AP=1×3=3,
∴OP=OA+AP=1+3=4,
∴点P的坐标是(0,4).
把(0,4)代入y=﹣x+b,得b=4,
∴y=﹣x+4;
(3)解:当直线y=﹣x+b过M(3,2)时,2=﹣3+b,解得b=5,5=1+t1,解得t1=4,
当直线y=﹣x+b过N(4,4)时,4=﹣4+b,解得b=8,8=1+t2,解得t2=7,
t2﹣t1=7﹣4=3秒
(4)(4,0)或(﹣4,0)
【解析】解:(1)当t=2时,AP=1×2=2,
∵OP=OA+AP=3,
∴点P的坐标是(0,3);(4)设点Q的坐标为(x,0),
∵S△ONQ=8,
∴ ![]() |x|4=8,
|x|4=8,
解得x=±4,
∴点Q的坐标是(4,0)或(﹣4,0).
所以答案是3,(0,3);(4,0)或(﹣4,0).

练习册系列答案
相关题目