题目内容
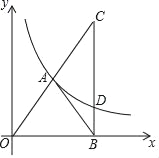
【题目】已知:如图,反比例函数y=![]() 的图象上的一点A(m,n)在第一象限内,点B在x轴的正半轴上,且AB=AO,过点B作BC⊥x轴,与线段OA的延长线相交于点C,与反比例函数的图象相交于点D.
的图象上的一点A(m,n)在第一象限内,点B在x轴的正半轴上,且AB=AO,过点B作BC⊥x轴,与线段OA的延长线相交于点C,与反比例函数的图象相交于点D.
(1)用含m的代数式表示点D的坐标;
(2)求证:CD=3BD;
(3)联结AD、OD,试求△ABD的面积与△AOD的面积的比值.
【答案】(1)D(2m,![]() );(2)详见解析;(3)
);(2)详见解析;(3)![]() .
.
【解析】
(1)先用m表示点A的坐标,进而利用等腰三角形的性质得出点B的坐标,即可得出结论;
(2)先确定出直线OA的解析式,即可得出点C的坐标,求出CD,BD即可得出结论;
(3)先判断出S△ACD=3S△ABD,再判断出S△AOD=S△ACD,即可得出结论.
(1)如图,
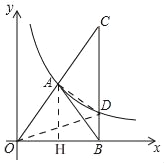
∵点A(m,n)在反比例函数y=![]() 的图象上,
的图象上,
∴n=![]() ,
,
∴A(m,![]() ),
),
过点A作AH⊥x轴于H,
∴H(m,0),
∵AB=OA,
∴OB=2OH,
∴B(2m,0),
∵BD⊥x轴于D,
∴点D的横坐标为2m,
∵点D在反比例函数y=![]() 的图象上,
的图象上,
∴D(2m,![]() );
);
(2)设直线AO的解析式为y=kx,
∵点A(m,![]() ),
),
∴![]() ,
,
∴k=![]() ,
,
∴直线AO的解析式为y=![]() x,
x,
∵点C在直线AO上,且横坐标为2m,
∴C(2m,![]() ),
),
∴CD=![]() ,
,
∵BD=![]() ,
,
∴CD=3BD;
(3)由(2)知,CD=3BD,
∴S△ACD=3S△ABD,
∵AB=AO,
∴∠AOB=∠ABO,
∵∠CBO=90°,
∴∠AOB+∠C=90°,∠ABO+∠ABC=90°,
∴∠C=∠ABC,
∴AB=AC,
∴AC=AO,
∴S△AOD=S△ACD,
∴S△AOD=3S△ABD,
∴![]() .
.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】某市开展了“雷锋精神你我传承,关爱老人从我做起”的主题活动,随机调查了本市部分老人与子女同住情况,根据收集到的数据,绘制成如下统计图表(不完整) 老人与子女同住情况百分比统计表
老人与子女 | 同住 | 不同住 | 不同住 | 其他 |
A | 50% | B | 5% |
根据统计图表中的信息,解答下列问题: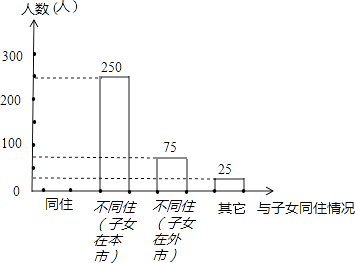
(1)求本次调查的老人的总数及a、b的值;
(2)将条形统计图补充完整;(画在答卷相对应的图上)
(3)若该市共有老人约15万人,请估计该市与子女“同住”的老人总数.


