Question

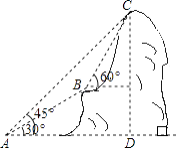
【题目】如图，在等边△ABC中，点D，E分别在边BC，AC上，且AE=CD，BE与AD相交于点P，BQ上AD于点Q．

(1)求证：AD=BE；

(2)求∠PBQ的度数；

(3)若PQ=3，PE=1，求AD的长．

Answer 1

【答案】（1）证明详见解析；（2）∠PBQ=30°；（3）AD=7.

【解析】

（1）根据等边三角形的性质，通过全等三角形的判定定理SAS证得△AEB≌△CDA，根据全等三角形的性质即可得到结论；

（2）利用（1）中的全等三角形的对应角相等和三角形外角的性质求得∠BPQ=60°，再由直角三角形两锐角互余即可得到结论；

（3）由“30度角所对的直角边是斜边的一半”得到2PQ=BP=6，则易求BE=BP+PE=7．

（1）∵△ABC为等边三角形，∴AB=CA，∠BAE=∠C=60°．

在△AEB与△CDA中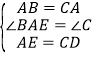，∵，∴△AEB≌△CDA（SAS），∴AD=BE；

（2）由（1）知，△AEB≌△CDA，则∠ABE=∠CAD，∴∠BAD+∠ABE=∠BAD+∠CAD=∠BAC=60°，∴∠BPQ=∠BAD+∠ABE=60°．

在Rt△PBQ中，∠PBQ=90°－∠BPQ=90°－60°=30°；

（3）∵∠PBQ=30°，∴PQ=BP=3，∴BP=6，∴BE=BP+PE=7，即AD=7．

故答案为：7．