题目内容
【题目】如图,某电信部门计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)?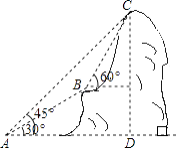
【答案】解:过B点分别作BE⊥CD、BF⊥AD,垂足分别为E、F.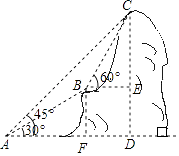
设BC=xm.
∵∠CBE=60°,
∴BE= ![]() x,CE=
x,CE= ![]() x.
x.
∵CD=200,
∴DE=200﹣ ![]() x.
x.
∴BF=DE=200﹣ ![]() x,DF=BE=
x,DF=BE= ![]() x.
x.
∵∠CAD=45°,
∴AD=CD=200.
∴AF=200﹣ ![]() x.
x.
在Rt△ABF中,tan30°= ![]() =
= 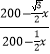 ,
,
解得,x=200( ![]() ﹣1)≈147m,
﹣1)≈147m,
答:电缆BC至少长147米.
【解析】过B点分别作BE⊥CD、BF⊥AD,垂足分别为E、F.设BC=xm,用x表示出BE、CE,根据题意求出AF、BF,根据正切的定义列出算式,求出x即可.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目