题目内容
【题目】已知:在四边形ABCD中,∠ABC=∠ADC=90,M、N分别是CD和BC上的点.
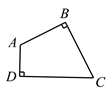
求作:点M、N,使△AMN的周长最小.
作法:如图,
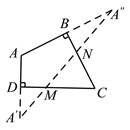
(1)延长AD,在AD的延长线上截取DA=DA;
(2)延长AB,在AB的延长线上截取B A″=BA;
(3)连接A′A″,分别交CD、BC于点M、N.则点M、N即为所求作的点.
请回答:这种作法的依据是_____________.
【答案】①线段垂直平分线的定义(或线段垂直平分线的判定,或轴对称的性质即对称点的连线段被对称轴垂直平分)
②线段垂直平分线上的点到线段两个端点的距离相等(线段垂直平分线的性质);
③两点之间线段最短.
【解析】分析:分别作出点A关于CD,BC的对称点A′,A″,连接A′A″分别交CD、BC于点M、N此时△AMN周长最小.
详解:作图的依据是:①线段垂直平分线的定义(或线段垂直平分线的判定,或轴对称的性质即对称点的连线段被对称轴垂直平分)
②线段垂直平分线上的点到线段两个端点的距离相等(线段垂直平分线的性质);
③两点之间线段最短.
故答案为:①线段垂直平分线的定义(或线段垂直平分线的判定,或轴对称的性质即对称点的连线段被对称轴垂直平分)
②线段垂直平分线上的点到线段两个端点的距离相等(线段垂直平分线的性质);
③两点之间线段最短.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目