��Ŀ����
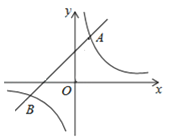
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ��ֱ���x�ᣬy���������քe���ڵ�A��B��AB=2![]() ����OAB=45��
����OAB=45��
��1����һ�κ����Ľ���ʽ��
��2������ڵڶ���������һ��C(a��![]() )�����ú���a�Ĵ���ʽ��ʾ�ı���ABCO����������������ABC���������ABO��������ʱa��ֵ��
)�����ú���a�Ĵ���ʽ��ʾ�ı���ABCO����������������ABC���������ABO��������ʱa��ֵ��
��3����x���ϣ��Ƿ���ڵ�P��ʹ��PABΪ���������Σ������ڣ���ֱ��д�����з��������ĵ�P���ꣻ�������ڣ���˵�����ɣ�
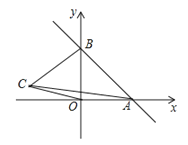
���𰸡���1��һ�κ�������ʽΪy= -x+2 ��2��a��![]() ��3�����ڣ����������ĵ�P������Ϊ��0��0����22
��3�����ڣ����������ĵ�P������Ϊ��0��0����22![]() ��0����2
��0����2![]() +2��0����-2��0����
+2��0����-2��0����
��������
��1�����ݹ��ɶ������A��B�������꣬���ô���ϵ�������ɽ�����⣻
��2������S�ı���ABCD=S��AOB+S��BOC���㼴�ɣ��г����̼������a��ֵ��
��3���������������ۼ��ɽ�����⣻
��1����Rt��ABO����OAB=45����
���OBA=��OAB-��OAB=90��-45��=45��
���OBA=��OAB
��OA=OB
��OB2+OA2=AB2����2OB2=��2![]() ��2��
��2��
��OB=OA=2
���A��2��0����B��0��2����
��![]()
��ã�![]()
��һ�κ�������ʽΪy= -x+2��
��2����ͼ��
��S��AOB=![]() ��2��2=2��S��BOC=
��2��2=2��S��BOC=![]() ��2��|a|= -a��
��2��|a|= -a��
��S�ı���ABCD=S��AOB+S��BOC=2-a��
��S��ABC=S�ı���ABCO-S��AOC=2-a-![]() ��2��
��2��![]() =
=![]() -a��
-a��
����ABC���������ABO������ʱ��![]() a��2�����a��
a��2�����a��![]() ��
��
��3����x���ϣ����ڵ�P��ʹ��PABΪ����������
�ٵ�PA=PBʱ��P��0��0����
�ڵ�BP=BAʱ��P��-2��0����
�۵�AB=APʱ��P��2-2![]() ��0����2+2
��0����2+2![]() ��0����
��0����
�������������������ĵ�P������Ϊ��0��0����22![]() ��0����2
��0����2![]() +2��0����-2��0����
+2��0����-2��0����