��Ŀ����
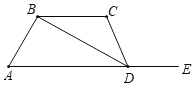
����Ŀ������ˮ������գ�A��B����ˮ�����طֱ��ջ�ˮ��380����320�����������Щˮ��ȫ�������ס��������۵㣬��A���������ס��������۵�ķ��÷ֱ�Ϊÿ��40Ԫ��20Ԫ����B���������ס��������۵�ķ��÷ֱ�Ϊÿ��15Ԫ��30Ԫ���ּ����۵���Ҫˮ��400���������۵���Ҫˮ��300����
��1�����A�������������۵�ˮ��x�������˷�ΪWԪ�����ú�x�Ĵ���ʽ��ʾW����д��x��ȡֵ��Χ��
��2�������˷Ѳ�����18300Ԫ����A�����������۵��ˮ��������200������ȷ���˷���͵����䷽�������������˷ѣ�
���𰸡���1��W=35x+11200��x��ȡֵ��Χ��80��x��380����2����A�������������۵��ˮ��200�������������۵��ˮ��180������B�������������۵��ˮ��200�������������۵��ˮ��120����
��������
���⣨1����x��ʾ����A�������������۵��ˮ����������B���������ס����������۵��ˮ��������Ȼ������˷�=������������ʽ�������ɵý⣬�ٸ�������ˮ����������С��0�г�����ʽ���õ�x��ȡֵ��Χ����2������һ�κ�����������ȷ�����˷����ʱ�����䷽����Ȼ����⼴�ɣ�
���������
��1�������⣬�б���
A��380�� | B��320�� | |
�ף�400�� | x | 400-x |
�ң�300�� | 380-x | 320-(400-x)=x-80 |
��W=40x+20��(380-x)+15��(400-x)+30��(x-80)=35x+11200
��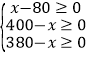 ���80��x��380
���80��x��380
��2�� �������![]() ���
���![]() ����x=200,201,202
����x=200,201,202
��w=35x+10,k=35��w��x���������������x=200ʱ���˷�w��ͣ�����˷�Ϊ81200Ԫ��
��ʱ���䷽�����£�
A | B | |
�� | 200 | 200 |
�� | 180 | 120 |

����Ŀ��ijʳƷ���������Ĵ�װʳƷ�г����Ʒ20�������ÿ���������Ƿ���ϱ�����������IJ��ֱַ���������������ʾ����¼���±���
��������IJ�ֵ����λ��g�� | ��5 | ��2 | 0 | 1 | 3 | 6 |
���� | 1 | 4 | 3 | 4 | 5 | 3 |
��1������������Ʒ��ƽ���������ж����ȱ������ػ�������٣�
��2����������Ϊ450�ˣ���������Ʒ���������Ƕ��٣�
��3��������ʳƷ�ĺϸ��Ϊ450��5�ˣ���������Ʒ�ĺϸ���Ϊ�� ����ֱ����д�𰸣�