[题目]如图.在△ABC中.AD是BC边上的中线.E是AD的中点.过点A作BC的平行线交BE的延长线于点F.连接CF．(1)求证:AF=DC ,(2)若∠BAC=.试判断四边形ADCF的形状.并证明你的结论．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

（1）求证：AF=DC ；

（2）若∠BAC=，试判断四边形ADCF的形状，并证明你的结论．

【答案】（1）证明见解析（2）菱形

【解析】试题分析：（1）根据AAS证△AFE≌△DBE，推出AF=BD，即可得出答案；
（2）得出四边形ADCF是平行四边形，根据直角三角形斜边上中线性质得出，根据菱形的判定推出即可．

试题解析：(1)证明：∵AF∥BC，

∴∠AFE=∠DBE，

∵E是AD的中点，AD是BC边上的中线，

∴AE=DE，BD=CD，

在△AFE和△DBE中

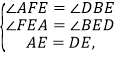
∴△AFE≌△DBE(AAS)，

∴AF=BD，

∴AF=DC.

(2)四边形ADCF是菱形，

证明：AF∥BC，AF=DC，

∴四边形ADCF是平行四边形，

∵AC⊥AB，AD是斜边BC的中线，

∴平行四边形ADCF是菱形.

练习册系列答案

相关题目

【题目】如图，在△ABC中，BD⊥AC，AB=6，，∠A=30°
（1）求AD和BC；
（2）求sin∠C．

【题目】图1所示矩形ABCD中，BC=x，CD=y，y与x满足的反比例函数关系如图2所示，等腰直角三角形AEF的斜边EF过C点，M为EF的中点，则下列结论正确的是

A. 当x=3时，EC＜EM B. 当y=9时，EC＞EM

C. 当x增大时，EC·CF的值增大。 D. 当y增大时，BE·DF的值不变。

【题目】如图，四边形ABCD是菱形，对角线AC，BD相交于点O，DH⊥AB于点H，连接OH，求证：∠DHO＝∠DCO.

【题目】（如图平面直角坐标系内,已知点A的坐标是(-3,0).

（1）点B的坐标为_______,点C的坐标为_____,∠BAC=______;

（2）求△ABC的面积;

（3）点P是y轴负半轴上的一个动点,连接BP交轴于点D,是否存在点P使得

△ADP与△BC的面积相等?若存在,请直接写出点P的坐标;若不存在,请说明理由.

【题目】如图，已知.试说明∥,请完成下列填空，把证明过程补充完整.

证明： ∵ __________________________ ，

∴ （_________________）.

∴

又∵

∴ __________________ （_____________________），

∴∥（_______________________________）.

【题目】请阅读求绝对值不等式和的解集过程：

对于绝对值不等式，从图1所示的数轴上看：大于而小于的数绝对值是小于的，所以的解集是；

对于绝对值不等式，从图2所示的数轴上看：小于而大于的数绝对值是大于的，所以的解集…….

解答下面的问题：

解不等式：⑴. ； ⑵. .

【题目】如图，在边长相同的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，AB，CD相交于点P，则的值= ， tan∠APD的值= ．

【题目】去年春季，蔬菜种植场在15公顷的大棚地里分别种植了茄子和西红柿，总费用是万元其中，种植茄子和西红柿每公顷的费用和每公顷获利情况如表：

	每公顷费用万元	每公顷获利万元
茄子
西红柿

请解答下列问题：

求出茄子和西红柿的种植面积各为多少公顷？

种植场在这一季共获利多少万元？

试题分类