题目内容
【题目】如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则 ![]() 的值= , tan∠APD的值= .
的值= , tan∠APD的值= . 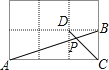
【答案】3;2
【解析】解: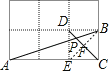
∵四边形BCED是正方形,
∴DB∥AC,
∴△DBP∽△CAP,
∴ ![]() =3,
=3,
连接BE,
∵四边形BCED是正方形,
∴DF=CF= ![]() CD,BF=
CD,BF= ![]() BE,CD=BE,BE⊥CD,
BE,CD=BE,BE⊥CD,
∴BF=CF,
根据题意得:AC∥BD,
∴△ACP∽△BDP,
∴DP:CP=BD:AC=1:3,
∴DP:DF=1:2,
∴DP=PF= ![]() CF=
CF= ![]() BF,在Rt△PBF中,tan∠BPF=
BF,在Rt△PBF中,tan∠BPF= ![]() =2,
=2,
∵∠APD=∠BPF,
∴tan∠APD=2,
故答案为:3,2.
首先连接BE,由题意易得BF=CF,△ACP∽△BDP,然后由相似三角形的对应边成比例,易得DP:CP=1:3,即可得PF:CF=PF:BF=1:2,在Rt△PBF中,即可求得tan∠BPF的值,继而求得答案.此题考查了相似三角形的判定与性质与三角函数的定义.此题难度适中,解题的关键准确作出辅助线,注意转化思想与数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?