Question

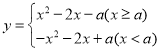【题目】函数（为常数）．

（1）若点在函数图象上，求的值；

（2）当时，若直线（为常数）与函数恰好有三个交点时，设三个交点的横坐标从左至右依次为、、，求的取值范围；

（3）已知、．若函数图象与线段有两个交点时，求的取值范围；

（4）当时，函数值满足，直接写出的取值范围．

Answer 1

【答案】（1）的值为-2或4；（2）；（3）或；（4） 或．

【解析】

（1）分和两种情况讨论，分别将代入对应的解析式求解即可；

（2）当时，若直线（为常数）与函数恰好有三个交点，则与直线有2个交点，即可得到，且直线位于顶点的下方，从而确定了m的取值，即可求得，从而得到结果；

（3）分情况讨论，当，此时两段抛物线各有一个交点，若，此时需与AB有2个交点，据此进行计算即可；

（4）分别讨论和两种情况，分别计算出当，时y的取值，然后计算判断范围即可．

解：（1）若，则将代入，

，解得，成立，

若，则将代入，

，解得，成立，

故的值为-2或4；

（2）当时，，

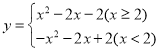的对称轴为，

∵ ，∴该图象仅有右半支的一部分，

时，

的对称轴为，

∵ ，∴该图象对称轴两侧均有图象，

时，

时，

在上，令，解得（舍），，

若直线（为常数）与函数恰好有三个交点时，

则，

∴，即， ，

∴，

∴；

（3）若，此时两段抛物线各有一个交点，

将代入，

解得，

若与AB有交点则

在，上，

若时，y=2，则，

解得 或，

若与AB有交点则，

∴；

若，此时需与AB有2个交点，

将代入，

解得，

由对称轴为直线，可知，若需与AB有2个交点，

则当y=2时，，

整理为，

则，解得，

∴，

综上所述，或；

（4）当时，在范围，

x=1，，

，，，

解得（舍）或，

，，，

解得，

∴，

当时，

x=-1，，满足范围，

因此x=2a，和x=2a+1时，，

在中，

，，，

解得，

，，，恒成立，

∵

∴

综上所述 或．