题目内容
【题目】定义:点P是四边形ABCD内一点,若三角形△PAB,△PBC,△PCD,△PDA均为等腰三角形,则称点P是四边形ABCD的一个“准中心”,如,正方形的中心就是它的一个“准中心”.
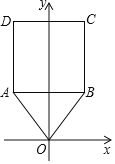
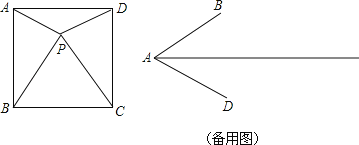
(1)如图,已知点P是正方形ABCD内的一点,且∠PBC=∠PCB=60°,证明点P是正四边形ABCD的一个“准中心”;
(2)填空:正方形ABCD共有 个“准中心”;
(3)已知∠BAD=60°,AB=AD=6,点C是∠BAD平分线上的动点,问在四边形ABCD的对角线AC上最多存在几个“准中心”点P(自行画出示意图),并求出每个“准中心”点P对应线段AC的长(精确到个位).
【答案】(1)证明见解析;(2)5;(3)在四边形ABCD的对角线AC上最多存在3个“准中心”点P;AC长为4![]() 或9或16.
或9或16.
【解析】
(1)根据正方形的性质,利用已知条件,即可解答;
(2)根据 “准中心”的定义即可求解;
(3)在四边形ABCD的对角线AC上最多存在3个“准中心”点P;分三种情况讨论:
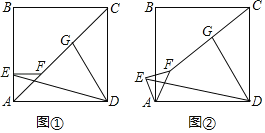
①如图1,当PA=PB=PC=PD时,点P是“准中心”点,
②如图2,当PA=BA=DA,PB=PC=PD时,点P是“准中心”点,
③如图3,当AB=PB=PC=PD=AD时,点P是“准中心”点,
利用角平分线的性质、等腰三角形的性质和解直角三角形,即可求出AC的长.
(1)∵ABCD为正方形,
∴∠ABC=∠BCD=∠CDA=∠DAB=90°,AB=BC=CD,
又∵∠PBC=∠PCB=60°,
∴∠BPC=60°,
∴PB=PC=BC=AB=CD,
∴PA=PD,
∴△PAB,△PBC,△PCD,△PDA均为等腰三角形,
∴点P是正方形ABCD的一个“准中心”.
(2)由(1)可知正方形ABCD有4个这样的“准中心”,再加上对角线的交点,即为5个“准中心”,
故答案为:5;
(3)在四边形ABCD的对角线AC上最多存在3个“准中心”点P;
①如图1,当PA=PB=PC=PD时,点P是“准中心”点,

∵∠BAD=60°,点C是∠BAD平分线上,
∴∠BAC=30°,
∴∠ACB=∠BPC=60°,∠ABC=90°,
则AC=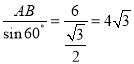 .
.
②如图2,当PA=BA=DA,PB=PC=PD时,点P是“准中心”点,
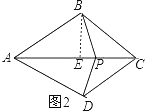
则PA=6,
∵∠BAD=60°,点C是∠BAD平分线上,
∴∠BAC=30°,
∴∠APB=75°,
∴∠PCB=![]() =37.5°,
=37.5°,
作BE⊥AC于点E,
在Rt△AEB中,BE=![]() AB=3,AE=AB
AB=3,AE=AB![]() ,
,
在Rt△CEB中,CE=![]() ,
,
∴AC=AE+CE=![]() .
.
③如图3,当AB=PB=PC=PD=AD时,点P是“准中心”点,

此时四边形ABPD是菱形,连接BD,
则PA=2AE=2ABcos30°=![]() ,
,
∴AC=PA+PC=![]() .
.
综上,在四边形ABCD的对角线AC上最多存在3个“准中心”点P;AC长为4![]() 或9或16.
或9或16.