题目内容
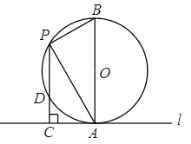
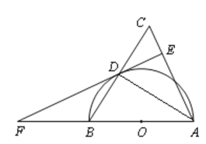
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)如果⊙O的半径为5,cos∠DAB=![]() ,求BF的长.
,求BF的长.
【答案】(1)见解析 (2)![]()
【解析】
(1)连接OD,AB为⊙O的直径得∠ADB=90°,由AB=AC,根据等腰三角形性质得AD平分BC,即DB=DC,则OD为△ABC的中位线,所以OD∥AC,而DE⊥AC,则OD⊥DE,然后根据切线的判定方法即可得到结论;
(2)由∠DAC=∠DAB,根据等角的余角相等得∠ADE=∠ABD,在Rt△ADB中,利用解直角三角形的方法可计算出AD=8,在Rt△ADE中可计算出AE=![]() ,然后由OD∥AE,得△FDO∽△FEA,再利用相似比可计算出BF.
,然后由OD∥AE,得△FDO∽△FEA,再利用相似比可计算出BF.
(1)证明:连接OD,如图,
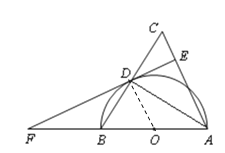
∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分BC,即DB=DC,
∵OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴EF是⊙O的切线;
(2)![]()
![]()
在Rt△ADB中,cos∠DAB=![]() ,而AB=10,
,而AB=10,
∴AD=8,
在Rt△ADE中,![]() ,
,
∴AE=![]() ,
,
∵OD∥AE,
∴△FDO∽△FEA,
∴![]() ,即
,即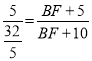 ,
,
∴![]()

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目