Question

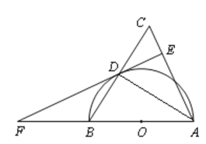
【题目】如图，已知半径为2的⊙O与直线l相切于点A，点P是直径AB左侧半圆上的动点，过点P作直线l的垂线，垂足为C，PC与⊙O交于点D，连接PA、PB，设PC的长为x（2＜x＜4），则PDCD的最大值是（　　）．

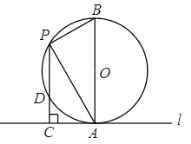
A.2B.3C.4D.6

Answer 1

【答案】A

【解析】

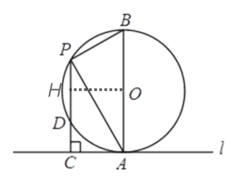
过点O向BC作垂线OH，垂足为H，由垂径定理得到H为PD的中点，设PC=x，根据CD=PC-PD，进而求出PD·CD，整理后得到关于x的二次函数，利用二次函数的性质即可求出所求式子的最大值及此时x的取值．

过点O向BC作垂线OH，垂足为H，

∵PD是⊙O的弦，OH⊥PD，

∴PH=HD.

∵∠CHO=∠HCA=∠OAC=90°，

∴四边形OACH为矩形，

∴CH=OA=2，

∵PC=x，

∴PH=HD=PC-CH=x-2，

∴CD=PC-PD=x-2(x-2)=4-x，

∴PD·CD=2 (x-2)(4-x)=-2x2+12x-16=-2(x-3)2+2，

∵2＜x＜4，

∴当x=3时，PD·CD的值最大，最大值是2，

故选：A．