Question

【题目】在平面直角坐标系中，已知直线与双曲线的一个交点是．

（1）求的值；

（2）设点是双曲线上不同于的一点，直线与轴交于点．

①若，求的值；

②若，结合图象，直接写出的值．

Answer 1

【答案】（1）．（2）①；②或.

【解析】

（1）由直线解析式求得A（2，1），然后代入双曲线y=中，即可求得k的值；

（2）①根据系数k的几何意义即可求得n的值，得到P的坐标，继而求得直线PA的解析式，代入B（b，0）即可求得b的值；②分两种情况讨论求得即可．

（1）∵直线y=x与双曲线y=的一个交点是A（2，a），

∴a=×2=1，

∴A（2，1），

∴k=2×1=2；

（2）①若m=1，则P（1，n），

∵点P（1，n）是双曲线y=上不同于A的一点，

∴n=k=2，

∴P（1，2），

∵A（2，1），

则直线PA的解析式为y=-x+3，

∵直线PA与x轴交于点B（b，0），

∴0=-b+3，

∴b=3；

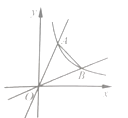
②如图1，当P在第一象限时，

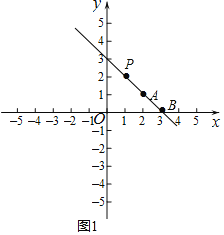
∵PB=2AB，A（2，1），

∴P点的纵坐标时2，

代入y=求得x=1，

∴P（1，2），

由①可知，此时b=3；

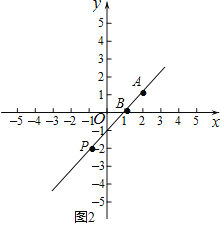
如图2，当P在第，三象限时，

∵PB=2AB，A（2，1），

∴P点的纵坐标时-2，

代入y=求得x=-1，

∴P（-1，-2），

∵A（2，1）

则直线PA的解析式为y=x-1，

∴b=1，

综上，b的值为3或1．