��Ŀ����
����Ŀ��������СԪ��Ƶġ���Բ��һ����Բ�����ߡ��ij߹���ͼ���̣�
��֪����ͼ����O����O��һ��P��
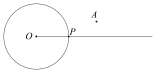
����������P�ġ�O�����ߣ�
��������ͼ��������OP��
�� ��ֱ��OP����ȡһ��A����AΪԲ�ģ�APΪ�뾶����A��������OP������һ��B��
�����Ӳ��ӳ�BA���A���ڵ�C��
����ֱ��PC��
��ֱ��PC��Ϊ������СԪ��Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤����
֤������ BC�ǡ�A��ֱ����
�� ��BPC=90�� �����������ݣ���
�� OP��PC��
�֡� OP�ǡ�O�İ뾶��
�� PC�ǡ�O������ �����������ݣ���
���𰸡���1������������2��ֱ�����Ե�Բ�ܽ���ֱ�ǣ����뾶��˲��Ҵ�ֱ�������뾶��ֱ����Բ������
��������
��1��������������ͼ�μ��ɣ�
��2������Բ�ܽǶ����õ���BPC=90�㣬�������ߵ��ж��������ɵõ����ۣ�
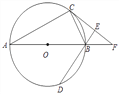
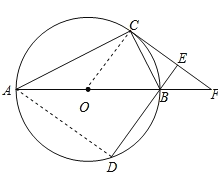
�⣺��1����ȫͼ����ͼ��ʾ����ֱ��PC��Ϊ����
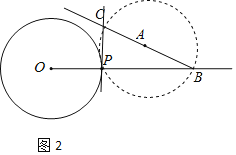
��2��֤������BC�ǡ�A��ֱ����
���BPC=90�㣨Բ�ܽǶ�������
��OP��PC��
�֡�OP�ǡ�O�İ뾶��
��PC�ǡ�O�����ߣ����ߵ��ж�����
�ʴ�Ϊ��Բ�ܽǶ��������ߵ��ж���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ