题目内容
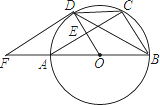
【题目】如图,AB是⊙O的直径,AC是弦,半径OD⊥AC于点E,过点D的切线与BA延长线交于点F.
(1)求证:∠CDB=∠BFD;
(2)若AB=10,AC=8,求DF的长.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)根据切线的性质得到DF⊥OD,由于OD⊥AC,推出DF∥AC,根据平行线的性质得到∠CAB=∠BFD,于是得到结论;
(2)利用垂径定理得出AE的长,再利用相似三角形的判定与性质得出FD的长.
试题解析:(1)∵DF与⊙O相切,
∴DF⊥OD,
∵OD⊥AC,
∴DF∥AC,
∴∠CAB=∠BFD,
∴∠CAB=∠CDB,
∴∠CDB=∠BFD;
(2)∵半径OD垂直于弦AC于点E,AC=8,
∴AE=![]() AC=
AC=![]() ×8=4.
×8=4.
∵AB是⊙O的直径,
∴OA=OD=![]() AB=
AB=![]() ×10=5,
×10=5,
在Rt△AEO中,OE=![]() =3,
=3,
∵AC∥DF,
∴△OAE∽△OFD.
∴![]() ,
,
∴![]() ,
,
∴DF=![]() .
.

练习册系列答案
相关题目