��Ŀ����
����Ŀ����һ�տ����������һ���Ϊ����ABCD��С�ݣ�AB+BC=10m��˩סС����10m��������һ�˹̶���B�㴦��С���ڲ��ܽ���С���ڵ������»������Ի���������ΪS��m2����
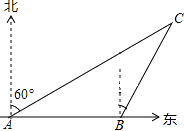
��1����ͼ1����BC=4m����S=m2 ��
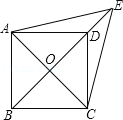
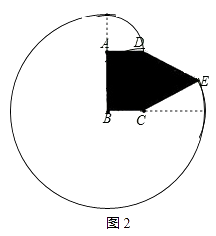
��2����ͼ2���ֿ����ڣ�1���еľ���ABCDС�ݵ��Ҳ���CDΪ����չһ����CDE����ʹ֮������Ϊ�����ABCED��С�ݣ������������䣬����BC�ı仯�����У���Sȡ����Сֵʱ����BC�ij�Ϊm��
���𰸡�
��1��88��
��2��![]()
���������⣺��1����ͼ1��˩סС����10m��������һ�˹̶���B�㴦��С�����Ի��������ͼ��ʾ��
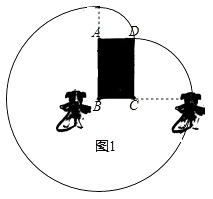
��ͼ��֪��С������������Ϊ��BΪԲ�ġ�10Ϊ�뾶�� ![]() Բ����CΪԲ�ġ�6Ϊ�뾶��
Բ����CΪԲ�ġ�6Ϊ�뾶�� ![]() Բ����AΪԲ�ġ�4Ϊ�뾶��
Բ����AΪԲ�ġ�4Ϊ�뾶�� ![]() Բ������ͣ���S=
Բ������ͣ���S= ![]() ����102+
����102+ ![]() ��62+
��62+ ![]() ��42=88��
��42=88��
�� 2 ����ͼ2����BC=x����AB=10��x����S= ![]() ��102+
��102+ ![]() ��x2+
��x2+ ![]() ��10��x��2
��10��x��2
= ![]() ��x2��10x+250��=
��x2��10x+250��= ![]() ��x2��5x+250������x=
��x2��5x+250������x= ![]() ʱ��Sȡ����Сֵ����BC=
ʱ��Sȡ����Сֵ����BC= ![]() ��
��
���Դ��ǣ�88�У� ![]() ��
��
�����㾫����������Ĺؼ�������������������㹫ʽ�����֪ʶ��������Բ�ϣ��������뾶��һ�λ�Χ�ɵ�ͼ�ν������Σ��������S=�У�R2-r2����