题目内容
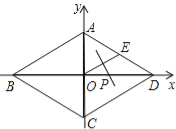
【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=12,BD=16,E为AD中点,点P在x轴上移动.若△POE为等腰三角形,请写出所有符合要求的点P的坐标 .

【答案】(2.5,0)或(-2.5,0)或(4,0)或(![]() ,0).
,0).
【解析】
试题根据菱形的对角线互相垂直平分求出OA、OD,再利用勾股定理列式求出AD,然后根据直角三角形斜边上的中线等于斜边的一半求出OE,然后分①OE=OP时,求出点P的坐标,②OE=PE时点P和点D重合,③OP=OE时,点P在OE的垂直平分线上,求出OP的长度,然后写出点P的坐标即可.
试题解析:∵在菱形ABCD中对角线AC=6,BD=8,
∴OA=3,OD=4,
∴AD=![]() =
=![]() ,
,
∵E为AD中点,
∴OE=![]() AD=
AD=![]() ×5=2.5,
×5=2.5,
①OE=OP时,OP=2.5,
∴点P的坐标为(2.5,0)或(-2.5,0),
②OE=PE时点P和点D重合,P(4,0),
③OP=PE时,点P在OE的垂直平分线,
∴OP=![]() (
(![]() ×5)÷
×5)÷![]() =
=![]() ,
,
点P(![]() ,0),
,0),
综上所述,点P的坐标为(2.5,0)或(-2.5,0)或(4,0)或(![]() ,0).
,0).

练习册系列答案
相关题目
【题目】学校为了解全校![]() 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
频道 | 新闻 | 体育 | 电影 | 科教 | 其他 |
人数 |
|
|
|
|
|
![]() 求调查的学生人数及统计图表中
求调查的学生人数及统计图表中![]() 的值;
的值;
![]() 求选择其他频道在统计图中对应扇形的圆心角的度数;
求选择其他频道在统计图中对应扇形的圆心角的度数;
![]() 求全校最爱选择电影频道的学生人数.
求全校最爱选择电影频道的学生人数.