题目内容
【题目】已知一个由正奇数排成的数阵.用如图所示的四边形框去框住四个数.

(1)若设框住四个数中左上角的数为n,则这四个数的和为 (用n的代数式表示);
(2)平行移动四边形框,若框住四个数的和为228,求出这4个数;
(3)平行移动四边形框,能否使框住四个数的和为508?若能,求出这4个数;若不能,请说明理由.
【答案】(1)4n+32;(2)49、51、63、65;(3)不能框住这样的四个数,使四个数的和为508.
【解析】
(1)设框住四个数中左上角的数为n,则右上角的数为n+2,左下角的数为n+14,右下角的数为n+2+14,求它们的和即可;
(2)框住四个数的和为228列方程求解即可;
(3)假设能使框住四个数的和为508,则可得n=119,这样左上角的数119在第10行第6列,所以不能框住.
(1) n+n+2+n+14+n+2+14=4n+32;
(2) 根据题意可得,4n+32=228 ,
解得,n=49,
∴这四个数分别是49、51、63、65;
(3)不能框住这样的四个数,使四个数的和为508,
理由:假设能框住这样的四个数,
则4n+32=508,解得n=119
而119=9×12+11=(10-1) ×12+11,
这样左上角的数119在第10行第6列,
所以不能框住这样的四个数,使四个数的和为508.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
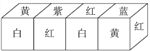
【题目】把正方体的六个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
现将上述大小相同,颜色、花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问:长方体的下底面共有多少朵花?