题目内容
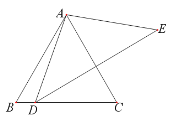
【题目】如图，△ABC是等边三角形，点D在BC上，△ADE是等腰三角形，AD ＝AE ，∠DAE ＝100°，当DE⊥AC时，求∠BAD和∠EDC的度数.
【答案】30°
【解析】
首先利用等边三角形的性质得出∠B=∠BAC=∠C=60°，再利用等腰三角形的性质得出∠ADE＝∠E＝40°，进而得出∠BAD=10°，进而利用三角形外角性质得出答案．
解：∵△ABC是等边三角形
∴∠B=∠BAC=∠C=60°
又∵AD =AE ，∠DAE =100°，
∴∠ADE=∠E =40°
∵DE⊥AC
∴ ∠DAC =∠EAC =50°
∴ ∠BAD=60°-50°=10°
又∵∠ADC=∠B +∠BAD =70°
∴∠EDC =∠ADC -∠ADE =30°
练习册系列答案
高中必刷题系列答案
相关题目
