题目内容
【题目】如图，在平面直角坐标系
中，
的
、
两个顶点在
轴上，顶点
在
轴的负半轴上．已知
，
，的面积
，抛物线
经过、、三点．
求此抛物线的函数表达式；
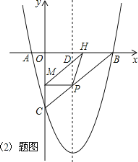
点
是抛物线对称轴上的一点，在线段
上有一动点
，以每秒
个单位的速度从
向运动，（不与点，重合），过点作
，交
轴于点
，设点的运动时间为
秒，试把
的面积
表示成的函数，当为何值时，有最大值，并求出最大值；
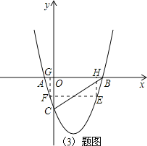
设点
是抛物线上异于点，的一个动点，过点作轴的平行线交抛物线于另一点
．以
为直径画
，则在点的运动过程中，是否存在与轴相切的？若存在，求出此时点的坐标；若不存在，请说明理由．
【答案】
；
当
时，
有最大值是
；
存在点
：
，
，
，
使得以
为直径的
与
轴相切．
【解析】
（1）由已知设OA＝m，则OB＝OC＝5m，AB＝6m，由S△ABC＝
AB×OC＝15，可求m的值，确定A、B、C三点坐标，由A、B两点坐标设抛物线交点式，将C点坐标代入求解即可；
（2）先根据点B、C的坐标求出直线BC的解析式，在设出点M的坐标，从而求出MH的解析式，根据抛物线的对称轴x＝2得到直线MH与对称轴的交点D的坐标，求出DP的长度，然后根据S△PMH＝S△PMD＋S△PDH，列式得到关于t的二次函数，最后根据二次函数的最值问题解答即可；（3）存在．根据抛物线的解析式设出点E的坐标，然后根据二次函数的对称性求出点E到对称轴的距离，再根据以EF为直径的⊙Q与x轴相切，则点E到x轴的距离等于点E到对称轴的距离相等，然后列出方程，再根据绝对值的性质去掉括号解方程即可，从而得到点E的坐标．
∵
，
，
设
，则
，
，
由
，得
，
解得
（舍去负值），
∴
，
，
，
设抛物线解析式为
，将
点坐标代入，得
，
∴抛物线解析式为
，
即
；
∵，，
∴直线
的解析式为：
，
∵点
的运动时间为
，
∴
，
∵直线
平行于直线，
∴直线为
，
设直线与对称轴交于点
，点的坐标为
，
∴
，
∴
，
，
∴当
时，
有最大值是；∵抛物线的解析式为，
∴设点
的坐标为
，
又∵抛物线的对称轴为
，
∴点到对称轴的距离为
，
∵以
为直径的
与
轴相切，
∴
，
①
，
时，即
时，
，
整理得，
，
解得
，
（舍去），
∴
，
此时点的坐标为，
②，
时，即
时，
，
整理得，
，
解得
，
（舍去），
∴
，
此时点的坐标为，
③
，时，即
时，
，
整理得，，
解得，（舍去），
∴
，
此时点的坐标为，
④，时，即
时，
，
整理得，，
解得，（舍去），
∴
，
此时点的坐标为，
综上所述，存在点：，，，使得以为直径的与轴相切．
