题目内容
【题目】如图,若![]() 是正数,直线
是正数,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ;直线
;直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ;抛物线
;抛物线![]() :
:![]() 的顶点为
的顶点为![]() ,且
,且![]() 与
与![]() 轴右交点为
轴右交点为![]() .
.
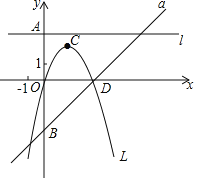
(1)若![]() ,求
,求![]() 的值,并求此时
的值,并求此时![]() 的对称轴与
的对称轴与![]() 的交点坐标;
的交点坐标;
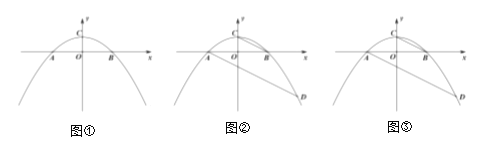
(2)当点![]() 在
在![]() 下方时,求点
下方时,求点![]() 与
与![]() 距离的最大值;
距离的最大值;
(3)设![]() ,点
,点![]() ,
,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 和
和![]() 上,且
上,且![]() 是
是![]() ,
,![]() 的平均数,求点
的平均数,求点![]() 与点
与点![]() 间的距离;
间的距离;
(4)在![]() 和
和![]() 所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出
所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出![]() 和
和![]() 时“美点”的个数.
时“美点”的个数.
【答案】(1)![]() ,
,![]() ;(2)1;(3)
;(2)1;(3)![]() ;(4)当
;(4)当![]() 时“美点”的个数为4040个,
时“美点”的个数为4040个,![]() 时“美点”的个数为1010个.
时“美点”的个数为1010个.
【解析】
(1)先求出A、B 的坐标,再由AB=8,可求出b的值,从而得到L的解析式,进而可求L的对称轴与a的交点;
(2)通过配方,求出L的顶点坐标,由于点C在l下方,则C与l的距离![]() ,配方即可得出结论;
,配方即可得出结论;
(3)由題意得y1+y2=2y3,进而可得b和x0的方程,解得x0的值,再求出L与x轴右交点D的坐标,即可得出结论;
(4)①当b=2019时,抛物线解析式L:y=﹣x2+2019x,直线a的解析式是:y=x﹣2019,由美点的定义可得美点的个数;②当b=2019.5时,抛物线解析式L:y=﹣x2+2019.5x,直线a的解析式是:y=x﹣2019.5,再由美点的定义即可得出美点的个数.
解:(1)当![]() 时,
时,![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() :
:![]() ,
,
∴![]() 的对称轴为直线
的对称轴为直线![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 的对称轴与
的对称轴与![]() 的交点为
的交点为![]() ;
;
(2)∵![]() ,∴
,∴![]() 的顶点
的顶点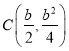 .
.
∵点![]() 在
在![]() 下方,∴
下方,∴![]() 与
与![]() 的距离是:
的距离是:![]() ,
,
∴点![]() 与
与![]() 距离的最大值为1;
距离的最大值为1;
(3)∵![]() 是
是![]() ,
,![]() 的平均数,∴
的平均数,∴![]() ,
,
∴![]() ,解得:
,解得:![]() 或
或![]() .
.
∵![]() ,∴
,∴![]() ,
,
对于![]() ,当
,当![]() 时,
时,![]() ,即
,即![]() ,解得:
,解得:![]() ,
,![]() .
.
∵![]() ,∴右交点
,∴右交点![]() ,
,
∴点![]() 与点
与点![]() 间的距离为
间的距离为![]() ;
;
(4)①当![]() 时,抛物线解析式
时,抛物线解析式![]() :
:![]() ,直线
,直线![]() 的解析式是:
的解析式是:![]() .
.
联立上述两个解析式可得:![]() ,
,![]() ,
,
∴可知每一个整数![]() 的值都对应着一个整数
的值都对应着一个整数![]() 值,且-1和2019之间(包括-1和2019)共有2021个整数;
值,且-1和2019之间(包括-1和2019)共有2021个整数;
∵另外要知道所围成的封闭图形边界分两部分:线段和拋物线,
∴线段和拋物线上各有2021个整数点,∴总计4042个点.
∵这两段图象交点有2个点重复,
∴“美点”的个数:![]() (个);
(个);
②当![]() 时,抛物线解析式
时,抛物线解析式![]() :
:![]() ,直线
,直线![]() 的解析式是:
的解析式是:![]() ,
,
联立上述两个解析式可得:![]() ,
,![]() ,
,
∵当![]() 取整数时,在一次函数
取整数时,在一次函数![]() 上,
上,![]() 取不到整数值,因此在该图象上“美点”为0,
取不到整数值,因此在该图象上“美点”为0,
在二次函数![]() 图象上,当
图象上,当![]() 为偶数时,函数值
为偶数时,函数值![]() 可取整数,可知-1到2019.5之间有1010个偶数,
可取整数,可知-1到2019.5之间有1010个偶数,
因此“美点”共有1010个.
故![]() 时“美点”的个数为4040个,
时“美点”的个数为4040个,![]() 时“美点”的个数为1010个.
时“美点”的个数为1010个.

 名校课堂系列答案
名校课堂系列答案