题目内容
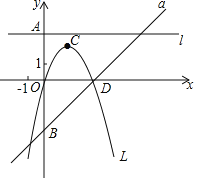
【题目】在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,顶点
两点,顶点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() .
.
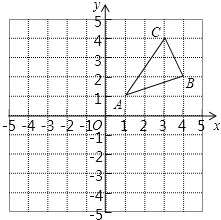
(1)如图①,求抛物线的解析式;
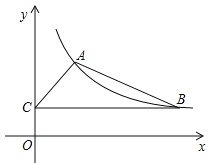
(2)如图②,连接![]() ,过点
,过点![]() 作
作![]() 的平行线,交第四象限的抛物线于点
的平行线,交第四象限的抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 在第四象限的抛物线上,过点
在第四象限的抛物线上,过点![]() 作
作![]() 于点
于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 、
、![]() ,且
,且![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)点D的坐标为(4,
;(2)点D的坐标为(4,![]() );(3)点K的坐标为:(3,1)或(3,2).
);(3)点K的坐标为:(3,1)或(3,2).
【解析】
(1)根据题意,设点C坐标为(0,4a),由![]() ,求出A、B两点坐标,利用待定系数法即可解决问题;
,求出A、B两点坐标,利用待定系数法即可解决问题;
(2)先求出直线BC的解析式,由AD∥BC,得到k相等,再把点A代入,得到直线AD的方程,然后与二次函数组成方程组,即可得到点D的坐标;
(3)根据题意,过点F作FL⊥x轴于L,根据平面直角坐标系中的解直角三角形,结合条件![]() ,得到边之间的关系,设点E为(m,
,得到边之间的关系,设点E为(m,![]() ),则HE=
),则HE=![]() ,OH=m,利用边之间的关系建立关于m的一元二次方程,即可求出m的值,即得到点K的横坐标,由
,OH=m,利用边之间的关系建立关于m的一元二次方程,即可求出m的值,即得到点K的横坐标,由![]() ,需进行分类讨论,即可得到答案.
,需进行分类讨论,即可得到答案.
解:(1)如图①,
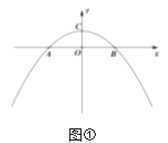
在![]() 中,设顶点C坐标为(0,4a),则OC=4a,
中,设顶点C坐标为(0,4a),则OC=4a,
∵![]() ,
,
∴OA=OB=2OC=8a,
∴点A坐标为(-8a,0),点B坐标为(8a,0),
把点B代入抛物线,得:![]() ,
,
解得:![]() 或
或![]() 或
或![]() ,
,
∵![]() ,则
,则![]() ,
,
∴![]() ,
,
∴抛物线的解析式为:![]() ;
;
(2)如图②,连接![]() ,过点
,过点![]() 作
作![]() 的平行线,交第四象限的抛物线于点
的平行线,交第四象限的抛物线于点![]() ,
,
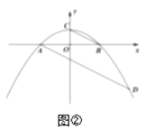
由(1)知,抛物线为![]() ,
,
∴点C坐标为(0,1),点B为(2,0),点A为(![]() ,0),
,0),
设直线BC的解析式为![]() ,
,
∴![]() ,解得:
,解得: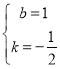 ,
,
∴直线BC的解析式为:![]() ;
;
∵AD∥BC,
∴设直线AD的解析式为![]() ,
,
把点A代入,得:![]() ,
,
∴![]() ,
,
∴直线AD的解析式为:![]() ;
;
∴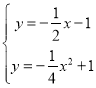 ,解得:
,解得: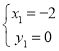 或
或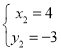 ,
,
∴点D的坐标为:(4,![]() );
);
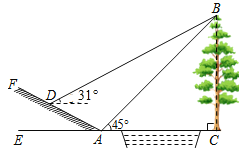
(3)如图,过点F作FL⊥x轴于L,
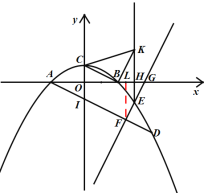
由(2)可知,直线AD为![]() ,
,
∴点I的坐标为:(0,![]() ),
),
∴OI=1,OA=2,
∴![]() .
.
∵FL⊥x轴,EH⊥x轴,EF⊥AD,
∴∠OAI+∠AGF=∠GEH+∠AGF=∠GFH+∠AGF=90°,
∴∠OAI =∠GEH=∠GFH,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ;
;
∴![]() ,
,
设点E坐标为(m,![]() ),
),
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴ ![]() ,
,
整理得:![]() ,
,
解得:![]() 或
或![]() (舍去);
(舍去);
∴点E的坐标为:(3,![]() );
);
∴点H为(3,0),点K的横坐标为3,
∴BH=1=OC,
①当CK平行x轴时,∠HBK=∠BKC=45°,
此时△BHK是等腰直角三角形,
∴HK=BK=1,
∴点K的坐标为(3,1);
②当△BKC时等腰直角三角形时,∠BKC=45°,则BC=BK,
∴△OBC≌△HKC(HL),
∴HK=OB=2,
∴点K的坐标为(3,2);
综合上述,点K的坐标为:(3,1)或(3,2).