题目内容
2.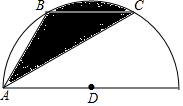 某工件形状如图(阴影部分),圆弧BC的度数为60°,且BC∥AD,BC=6cm,求阴影的面积.
某工件形状如图(阴影部分),圆弧BC的度数为60°,且BC∥AD,BC=6cm,求阴影的面积.小明同学是这样思考的:由BC∥AD,可得S△ABC=S△DBC,那么,阴影面积=6π.请你根据小明同学的思路帮他计算出阴影面积.
分析 连接BD、DC,根据平行线的性质得到S△ABC=S△DBC,根据扇形面积公式计算即可.
解答 解:连接DB、DC,
∵BC∥AD,
∴S△ABC=S△DBC,
∴阴影面积=扇形DBC的面积=$\frac{60π×{6}^{2}}{360}$=6π,
故答案为:S△DBC;6π.
点评 本题考查的是扇形面积的计算、平行线的性质,掌握扇形面积公式:S=$\frac{nπ{R}^{2}}{360}$是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.一元二次方程x2-$\sqrt{2}$x+1=0的根的情况是( )
| A. | 无实数根 | B. | 有两个实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
1.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案,在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设小红在同一商场累计购物x元,其中x>100.
(1)根据题意,填写下表(单位:元)
(2)当x取何值时,小红在甲、乙两商场的实际花费相同?
(3)请你根据小红累计购物的金额选择花费较少的商场?
(1)根据题意,填写下表(单位:元)
| 累计购物实际花费 | 130 | 290 | … | x |
| 在甲商场 | 127 | 271 | … | 0.9x+10 |
| 在乙商场 | 126 | 278 | … | 0.95x+2.5 |
(3)请你根据小红累计购物的金额选择花费较少的商场?
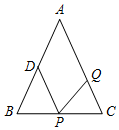 如图,等腰△ABC中,∠B=∠C,AB=AC=20cm,BC=16cm,点D为AB中点,如果点P在线段BC上以2cm/s 的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.当△BPD与△CQP全等时,点Q的运动速度为2或$\frac{5}{2}$cm/s.
如图,等腰△ABC中,∠B=∠C,AB=AC=20cm,BC=16cm,点D为AB中点,如果点P在线段BC上以2cm/s 的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.当△BPD与△CQP全等时,点Q的运动速度为2或$\frac{5}{2}$cm/s. 如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,求树高AB多少米.(结果保留根号)
如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,求树高AB多少米.(结果保留根号)