题目内容
【题目】已知椭圆E： 
=1（a＞b＞0）的左焦点F1（﹣ 
，0），若椭圆上存在一点D，满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F
（1）求椭圆E的方程；
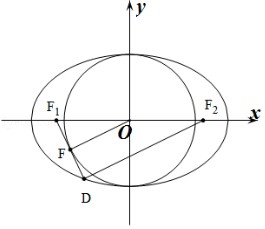
（2）过坐标原点O的直线交椭圆W： 
=1于P、A两点，其中点P在第一象限，过P作x轴的垂线，垂足为C，连结AC并延长交椭圆W于B，求证：PA⊥PB．
【答案】
（1）
解：连接DF2，FO（O为原点，F2为右焦点），由题意知：椭圆的右焦点为 
，
因为FO是△DF1F2的中位线，且DF1⊥FO，所以|DF2|=2|FO|=2b，
所以|DF1|=2a﹣|DF2|=2a﹣2b，故 
，
在Rt△FOF1中， 
，
即b2+（a﹣b）2=c2=5，又b2+5=a2，解得a2=9，b2=4，
所以椭圆E的方程为 
（2）
解：由（Ⅰ）得椭圆W的方程为 
，
设P（m，n），则A（﹣m，﹣n），C（m，0），
∴ 
， 
，直线 
，
联立方程组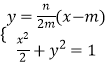 
，化简得 
，
∴ 
因为xA=﹣m，所以 
，则 
所以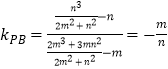 
，
则kPAkPB=﹣1，即PA⊥PB．
【解析】（I）用a，b，c表示出△OF1F的边长，利用勾股定理列方程解出a，b，即可；（II）设P（m，n），用m，n表示出直线AC的方程，求出B点坐标，计算PA，PB的斜率即可得出结论．
练习册系列答案
目标测试系列答案
相关题目
