��Ŀ����
����Ŀ����ͼ����A��1��0����B��3��0����x��Ĵ��ߣ��ֱ�ֱ��y=4��x��C��D���㣮������y=ax2+bx+c����O��C��D���㣮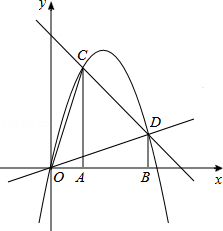
��1���������ߵı���ʽ��
��2����MΪֱ��OD�ϵ�һ�����㣬��M��x��Ĵ��߽��������ڵ�N�����Ƿ���������ĵ�M��ʹ����A��C��M��NΪ������ı���Ϊƽ���ı��Σ������ڣ����ʱ��M�ĺ����ꣻ�������ڣ���˵�����ɣ�
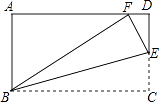
��3������AOC��CD����ƽ�ƣ���C���߶�CD�ϣ��Ҳ����D�غϣ�����ƽ�ƵĹ����С�AOC���OBD�ص����ֵ������ΪS������S�����ֵ��
���𰸡�
��1��
�⣺�����⣬�ɵ�C��1��3����D��3��1����
�������߹�ԭ�㣬���������ߵĽ���ʽΪ��y=ax2+bx��
�� ![]() ��
��
��� 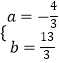 ��
��
�������ߵı���ʽΪ��y=�� ![]() x2+
x2+ ![]() x
x
��2��
�⣺���ڣ�
��ֱ��OD����ʽΪy=kx����D��3��1�����룬
���k= ![]() ��
��
��ֱ��OD����ʽΪy= ![]() x��
x��
���M�ĺ�����Ϊx����M��x�� ![]() x����N��x����
x����N��x���� ![]() x2+
x2+ ![]() x����
x����
��MN=|yM��yN|=| ![]() x������
x������ ![]() x2+
x2+ ![]() x��|=|
x��|=| ![]() x2��4x|��
x2��4x|��
�����⣬��֪MN��AC����Ϊ��A��C��M��NΪ������ı���Ϊƽ���ı��Σ�����MN=AC=3��
��| ![]() x2��4x|=3��
x2��4x|=3��
�� ![]() x2��4x=3�������ã�4x2��12x��9=0��
x2��4x=3�������ã�4x2��12x��9=0��
��ã�x= ![]() ��x=
��x= ![]() ��
��
�� ![]() x2��4x=��3�������ã�4x2��12x+9=0��
x2��4x=��3�������ã�4x2��12x+9=0��
��ã�x= ![]() ��
��
��������������ĵ�M����M�ĺ�����Ϊ�� ![]() ��
�� ![]() ��
�� ![]()
��3��
�⣺��C��1��3����D��3��1��
����ֱ��OC�Ľ���ʽΪy=3x��ֱ��OD�Ľ���ʽΪy= ![]() x��
x��
����ͼ��ʾ��
��ƽ���е�������Ϊ��A��O��C�䣬��C�����߶�CD�ϣ�
��O��C����x�ύ�ڵ�E����ֱ��OD���ڵ�P��
��A��C����x�ύ�ڵ�F����ֱ��OD���ڵ�Q��
��ˮƽ�����ƽ�ƾ���Ϊt��0��t��3����
��ͼ��AF=t��F��1+t��0����Q��1+t�� ![]() +
+ ![]() t����C�䣨1+t��3��t����
t����C�䣨1+t��3��t����
��ֱ��O��C��Ľ���ʽΪy=3x+b��
��C�䣨1+t��3��t������ã�b=��4t��
��ֱ��O��C��Ľ���ʽΪy=3x��4t��
��E�� ![]() t��0����
t��0����
����y=3x��4t��y= ![]() x�����x=
x�����x= ![]() t��
t��
��P�� ![]() t��
t�� ![]() t����
t����
����P��PG��x���ڵ�G����PG= ![]() t��
t��
��S=S��OFQ��S��OEP= ![]() OFFQ��
OFFQ�� ![]() OEPG
OEPG
= ![]() ��1+t����
��1+t���� ![]() +
+ ![]() t����
t���� ![]()
![]() t
t ![]() t
t
=�� ![]() ��t��1��2+
��t��1��2+ ![]()
��t=1ʱ��S�����ֵΪ ![]() ��
��
��S�����ֵΪ ![]() ��
��

����������1�����ô���ϵ������������ߵĽ���ʽ����2�������⣬��֪MN��AC����Ϊ��A��C��M��NΪ������ı���Ϊƽ���ı��Σ�����MN=AC=3�����M�ĺ�����Ϊx�������MN=| ![]() x2��4x|���ⷽ��|
x2��4x|���ⷽ��| ![]() x2��4x|=3�����x��ֵ������M�������ֵ����3����ˮƽ�����ƽ�ƾ���Ϊt��0��t��3��������ƽ���������S�ı���ʽ��S=��
x2��4x|=3�����x��ֵ������M�������ֵ����3����ˮƽ�����ƽ�ƾ���Ϊt��0��t��3��������ƽ���������S�ı���ʽ��S=�� ![]() ��t��1��2+
��t��1��2+ ![]() ����t=1ʱ��s�����ֵΪ
����t=1ʱ��s�����ֵΪ ![]() ��
��
�����㾫����ͨ��������ö��κ�����ͼ��Ͷ��κ��������ʣ����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С�����Խ����⣮

 ÿ�α���ϵ�д�
ÿ�α���ϵ�д�