题目内容
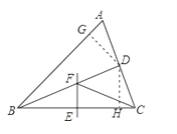
【题目】如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.
(1)若∠A=60°,∠ABD=24°,求∠ACF的度数;
(2)若EF=4,BF:FD=5:3,S△BCF=10,求点D到AB的距离.

【答案】(1)48°;(2)![]()
【解析】试题分析:(1)先根据角平分线的性质, ∠ABD=24°,可求出∠ABC=2∠ABD=48°,再根据三角形内角和的定理可得: ∠ACB=72°,再根据垂直平分线的性质可求出∠FCB=∠DBC=24°,即可求解,(2)先过D作DG⊥AB于G,DH⊥BC于H,根据相似三角形的判定可判定△BEF∽△BHD,根据相似三角形的性质可得对应边成比例,可求出DH,即可求解.
试题解析:(1)∵BD平分∠ABC,∠ABD=24°,
∴∠ABC=2∠ABD=48°,∠DBC=∠ABD=24°,
∵∠A=60°,
∴∠ACB=180°﹣∠A﹣∠ACB=180°﹣60°﹣48°=72°,
∵FE是BC的中垂线,
∴FB=FC,
∴∠FCB=∠DBC=24°,
∴∠ACF=∠ACB﹣∠FCB=72°﹣24°=48°,
(2)过D作DG⊥AB于G,DH⊥BC于H,
∵BD平分∠ABC,
∴DG=DH,
∵EF⊥BC,
∴EF∥DH,
∴△BEF∽△BHD,
∴![]() ,
,
∵EF=4,BF:FD=5:3,
∴DH=![]() .
.
∴DG=DH=![]() ,
,
∴点D到AB的距离=![]() .
.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目