��Ŀ����
����Ŀ������֪��ƽ���ı����кܶ����ʣ�����������ǰ�ƽ���ı�����������һ���Խ��߷��ۣ��ᷢ�������л��и���Ľ��ۣ�
�����ֽ��ۣ�
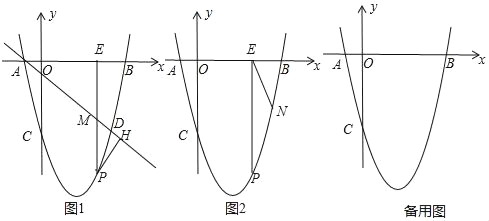
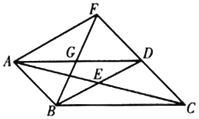
��1����ͼ������ABCD�У�AB��BC������ABC��AC��������AB��C������B��D������������Ȥ�Ľ��ۣ�����EAC�ǵ��������� ��AC//B��D ����ѡ������һ�����ۼ���֤��
���������ã�
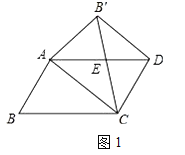
��2������ABCD�У���֪��BC=2����B=60��������ABC��AC��������AB��C������B��D������ͼ�������ı���ACDB���Ǿ��Σ���AC�ij���
��������չ��
��3���� ![]() =k������A��C��D��B��Ϊ������ı���Ϊ�����Σ���k��ֵΪ ��
=k������A��C��D��B��Ϊ������ı���Ϊ�����Σ���k��ֵΪ ��
���𰸡���1��֤������������2��![]() ����3��k��ֵΪ1��
����3��k��ֵΪ1��![]() .
.
��������
��1������ƽ���ı��ε����ʵó���EAC����ACB���ɷ��۵����ʵó���ACB����ACB����֤����EAC����ACB�����ó�AE��CE���ɣ���ͬ��֤��AE��CE��Ȼ�����DE��B��E��֤����CB��D����B��DA���ɡ�AEC����B��ED���ó���ACB������CB��D�����ɵó�AC//B��D��
��2���ɾ��ε����ʿɵá�BAC��90����Ȼ�����ú�30��ֱ�������ε����ʺ��ɶ�����⼴�ɣ�
��3��������������ۣ��ֱ�����ͼ�Σ����ݵ���ֱ�������ε�������⼴��.
�⣺��1��ѡ���ۢ٣�
֤�������ı���ABCD��ƽ���ı��Σ�
��AD��BC��AD��BC��
���EAC����ACB��
�ɷ��۵����ʵã���ACB����ACB����BC��B��C��
���EAC����ACB����
��AE��CE������ACE�ǵ��������Σ�
ѡ���ۢڣ�
֤�������ı���ABCD��ƽ���ı��Σ�
��AD��BC��AD��BC��
���EAC����ACB��
�ɷ��۵����ʵã���ACB����ACB����BC��B��C��
���EAC����ACB����
��AE��CE��
��DE��B��E��
���CB��D����B��DA��
�ߡ�AEC����B��ED��
���ACB������CB��D��
��AC//B��D��
��2����ͼ1��ʾ��
���ı���ACDB���Ǿ��Σ�
���CAB����90����
���BAC��90����
�ߡ�B��60����BC=2��
��AB��1��
��![]() ��
��
��3�������������
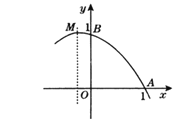
����ͼ2��ʾ��
���ı���ACDB���������Σ�
��AB����AC��
��AB����AB��
��AB��AC����![]() ��
��
����ͼ3��ʾ��
���ı���ACB��D�������Σ�
���AB��B��45������ACB����90����
��AB����AB��
���B��45������ACB��90����
����ABC�ǵ���ֱ�������Σ�
��![]() ��
��
����������k��ֵΪ1��![]() .
.