题目内容
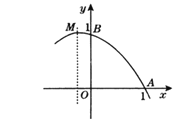
【题目】二次函数y=ax2＋bx＋c图象的一部分如图所示．已知它的顶点M在第二象限，且经过点A(1，0)和点B(0，l)．若此二次函数的图象与x轴的另一个交点为C.
（1）试求a，b所满足的关系式；
（2）当△AMC的面积为△ABC面积的
倍时，求a的值；
（3）是否存在实数a，使得△ABC为直角三角形．若存在，请求出a的值；若不存在，请说明理由．
【答案】 （1）a＋b=－1；（2）a=－4＋
；（3）不存在.
【解析】
（1）把点A（1，0）和点B（0，1）的坐标代入抛物线的解析式，就可以得到关于a，b，c关系式．整理就得到a，b的关系．
（2）利用公式求出抛物线的顶点的纵坐标，进而表示出△AMC的面积，根据
就可以得到关于a的方程，解得a的值；
（3）本题应分A是直角顶点，B是直角顶点，C是直角顶点三种情况进行讨论．
（1）将A（1，0），B（0，l）代入y=ax2＋bx＋c得：
，可得：a＋b=－1
（2）(2)∵a+b=1，
∴b=a1代入函数的解析式得到：y=ax2(a+1)x+1，
顶点M的纵坐标为
，
因为
由同底可知：
＝
整理得：a2＋8a＋1=0，得：a=－4±
由图象可知：a<0，因为抛物线过点（0，1），顶点M在第二象限，其对称轴x=
,
∴-1<a<0,
∴a=－4－舍去，从而a=－4＋
（3）① 由图可知，A为直角顶点不可能；
② 若C为直角顶点，此时与原点O重合，不合题意；
③ 若设B为直角顶点，则可知
，得：
令
，可得：
，
，
得：
，
∴
解得：a=-1，由－1＜a＜0，不合题意．所以不存在
综上所述：不存在.
【题目】某商贸公司有
、
两种型号的商品需运出，这两种商品的体积和质量分别如下表所示：
体积（立方米/件） | 质量（吨/件） | |
| 0．8 | 0．5 |
| 2 | 1 |
（1）已知一批商品有、两种型号，体积一共是20立方米，质量一共是10．5吨，求、两种型号商品各有几件？
（2）物资公司现有可供使用的货车每辆额定载重3．5吨，容积为6立方米，其收费方式有以下两种：
①按车收费：每辆车运输货物到目的地收费600元；
②按吨收费：每吨货物运输到目的地收费200元．
现要将（1）中商品一次或分批运输到目的地，如果两种收费方式可混合使用，商贸公司应如何选择运送、付费方式，使其所花运费最少，最少运费是多少元？
