题目内容
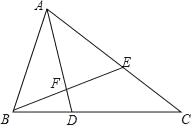
【题目】如图，直角三角形ABC有一外接圆，其中∠B=90°，AB＞BC，今欲在 
上找一点P，使得 
= 
，以下是甲、乙两人的作法： 甲：⑴取AB中点D
⑵过D作直线AC的平行线，交 于P，则P即为所求
乙：⑴取AC中点E
⑵过E作直线AB的平行线，交 于P，则P即为所求
对于甲、乙两人的作法，下列判断何者正确？（ ）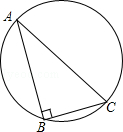
A.两人皆正确
B.两人皆错误
C.甲正确，乙错误C
D.甲错误，乙正确
【答案】D
【解析】解：（1）由甲的作法可知，DP是△ABC的中位线， ∵DP不垂直于BC，
∴ 
≠ 
；（2）由乙的作法，连BE，可知△BEC为等腰三角形
∵直线PE⊥BC，
∴∠1=∠2
故 = ；
∴甲错误，乙正确．
故选D．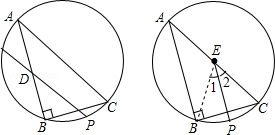
【考点精析】通过灵活运用三角形中位线定理和垂径定理，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧即可以解答此题．
练习册系列答案
相关题目
